|
|
Sacred Geometry, fractals and holographs, represent the the unification of everything. Until now we have had disjointed ideas about reality that don't see how everything is related and equal.
My Fractal Pattern Theory, or FPT is going to solve all of mankind's problems and make me rich famous. I think FPT is going to be so tantamount to our civilization that it will eventually lead to the ever elusive great unifying theory. It is a very simple theory but for some reason it doesn't appear to have been discovered yet. To me it looks like a ripe cherry of knowledge just starring me in the face as I happenstanced upon it. I feel very fortunate to have been the one to have discovered it; now I have to figure out a way to disseminate it.
The Fractal Pattern Theory obviously comes from fractals, so I will explain what they are first. A fractal is a beautiful natural phenomenon where a pattern
|
|
6 Nature
1 Astronomical Objects
| 1 Solar system plants diameter |
| 2 How waves Travel |
| 3 Lives of Stars |
|
| 2 Body |
| 3 Earth
|
|
6 Body
1 Introduction
|
| 2 I |
| 3 H |
| 4 C |
| 5 W |
| 6 A |
| 7 P |
|
|
1 Sacred Geometry
| 1 Interconnecting web of life
|
| 2 Vortex |
3 Theories
| 1 Unified field theory |
| 2 Particle in a Box |
| 3 Relativity & Quantum Mechanics |
| 4 Ptolemy's theorem |
|
| 4 Higher Dimensions |
| 5 Gravity VS Electromanetizm |
| 6 Swartzchild Equation |
| 7 Symmetry |
8 Dimensionality
| 1 Fractal |
| 2 Golden Ratio 1.618 |
|
9 Perfect Right Triangle
|
| 10 Gravitational singularity |
| 11 Curvature |
| 12 Naked Entropy |
| 13 Modern Progress |
| 14 Quantum Mechanics VS Classical Physics |
| 15 Mathematical Formulation |
| 16 Angles |
| 17 Radii, area, and volume |
| 18 Dual polyhedra |
| 19 Symmetry groups |
| 20 Technology |
| 21 Related Polyhedra & Polytopes |
| 22 Uniform Polyhedra |
| 23 Tessellations |
| 24 Computer generated fractals |
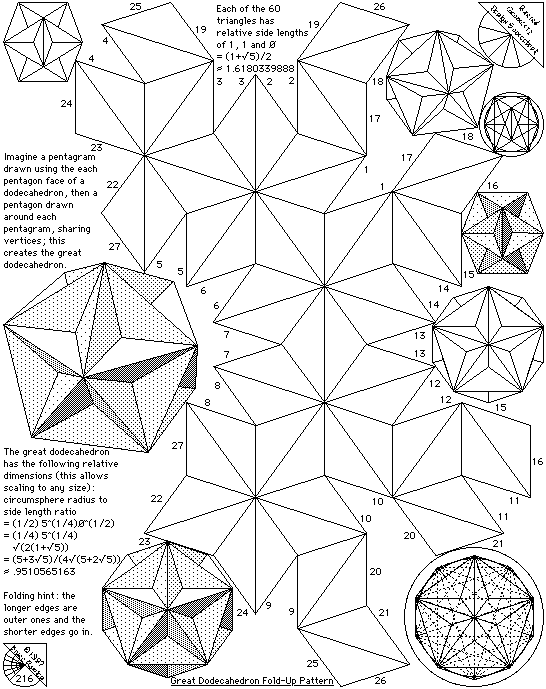
| 25 Golden triangle, pentagon and pentagram |
| 26 Scalenity of triangles |
| 27 Relationship to Fibonacci sequence |
| 28 Decimal expansion |
| 29 Mathematical pyramids and triangles technology |
| 30 Related polyhedra and polytopes |
| 31 Uniform polyhedra |
|
|
1 Architecture
|
2 Painting
1 Mandala
|
2 Religion
|
2 Buddhism
| 1 Early & Theravada |
| 2 Vajrayana |
| 3 Shingon |
| 4 Nichiren |
| 5 Pure Land |
|
3 Christianity
|
4 Bora ring |
|
|
3 Music |
|
|
| 1 Sphere |
| 2 Circle |
| 3 Point |
| 4 Square Root of 2 |
| 5 Spiral |
| 6 Torus |
| 7 Cone |
| 8 Metatron's Cube |
| 9 Pyramids |
|
5 About
1 Introduction
|
| 2 Interpretation |
| 3 History |
| 4 Current Status |
| 5 Worldview |
| 6 Applications |
| 7 Philosophical Consequences |
|
|
4 Types of Shapes
|
2 Archimedean Solid
| 1 truncated tetrahedron |
| 2 cuboctahedron |
| 3 truncated cube |
| 4 truncated octahedron |
| 5 rhombicuboctahedron |
| 6 truncated cuboctahedron |
| 7 snub cube |
| 8 icosidodecahedron |
| 9 truncated dodecahedron |
| 10 truncated icosahedron |
| 11 rhombicosidodecahedron |
| 12 truncated icosidodecahedron |
| 13 snub dodecahedron |
|
|
|
1 Sacred Geometry 

God is like a tree

Torus

Waves talking to each other

Polyhedron

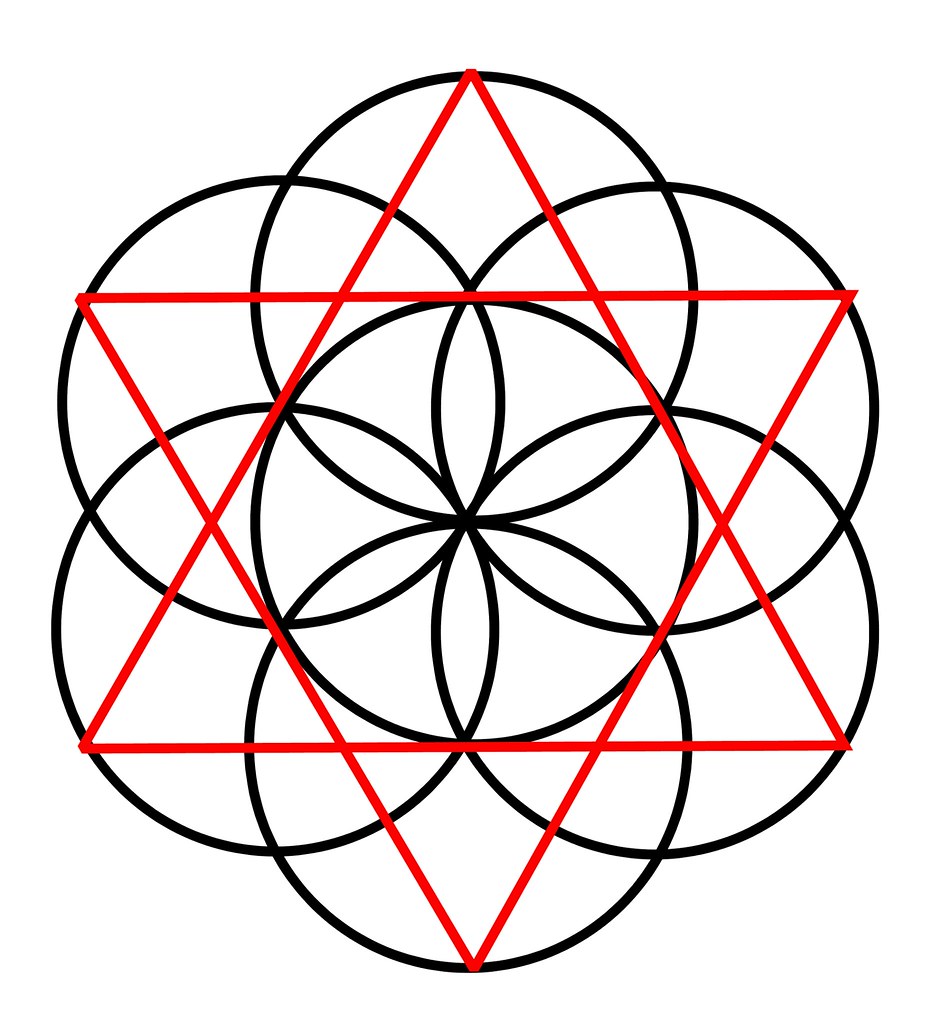
The flower of life
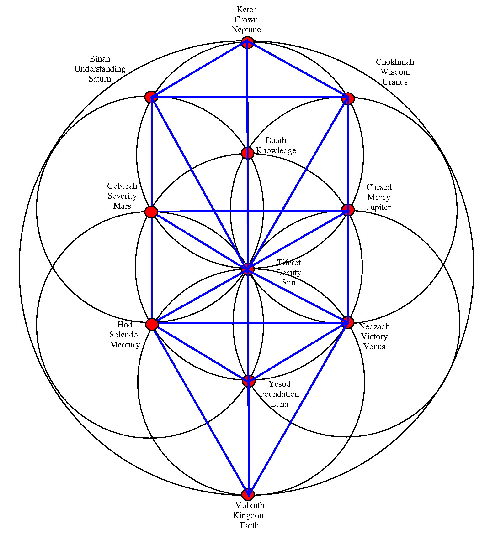
Flower of life and tree of life

Sextagon
OM
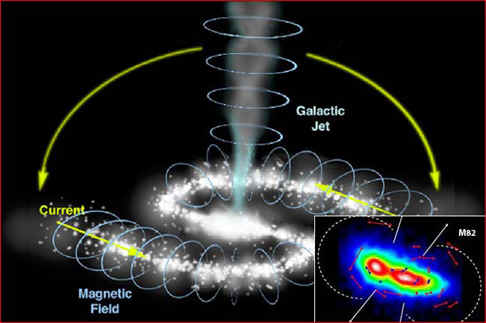
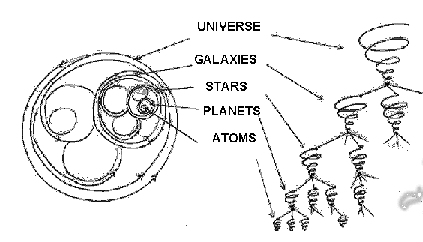
Galactic jet
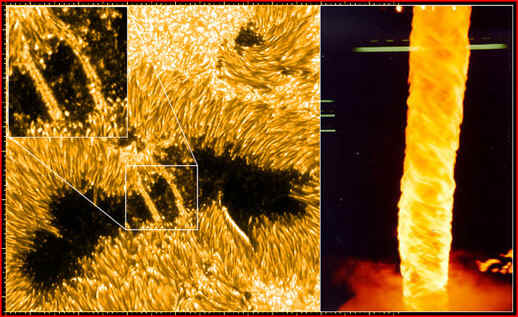
Twisting corona
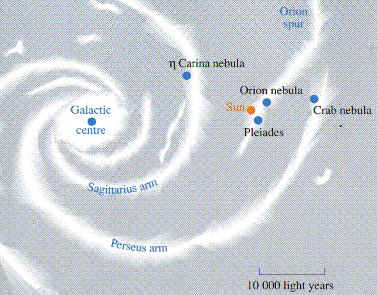
Our spiraling galaxy
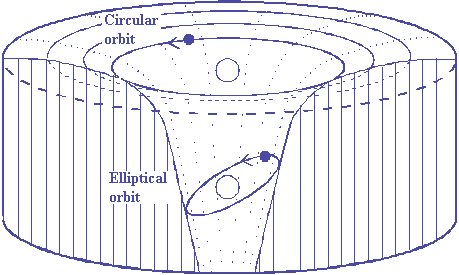
Space time
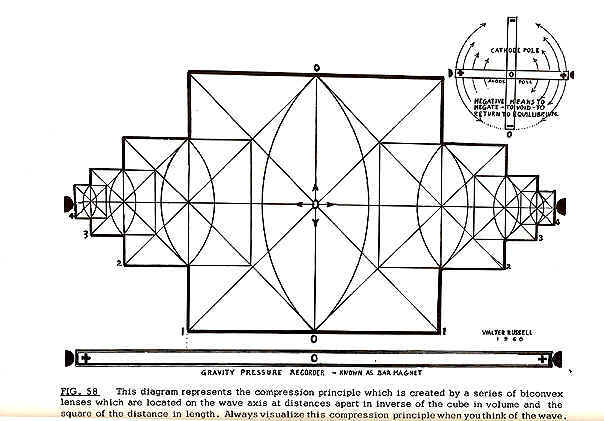

Wave travel

Cause of the Magnetosphere
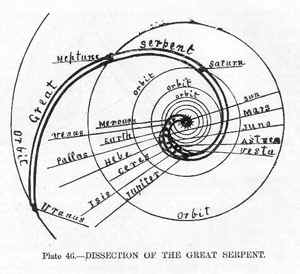
The solar system traveling though space
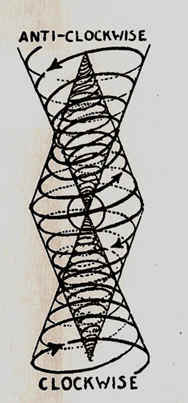
How energy spins in and out of the sphere
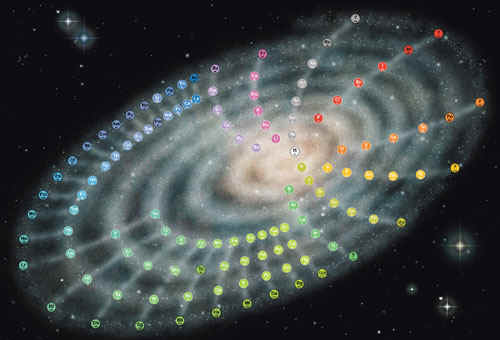
Spirla in the galaxy

Photos from the Bubble chamber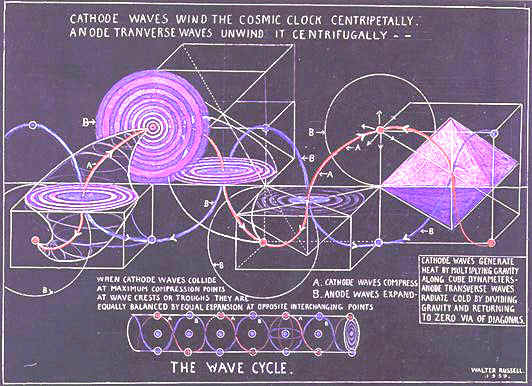
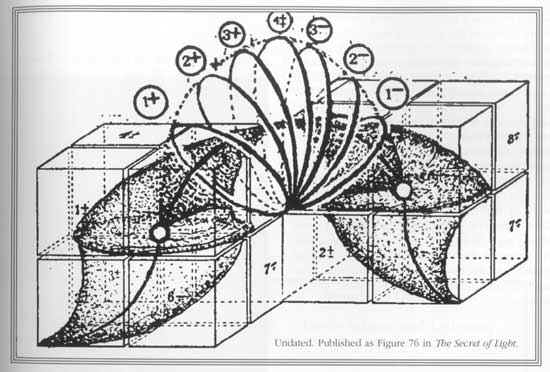



Torus

Torus dynamics

Eearth grid
Pentogram drawing
Sextogram and flower of life

Intricate flower of life

Sextogon inside Docegon
Septogram and Septogon

Tree of life point meanings
Septogram and Septogon
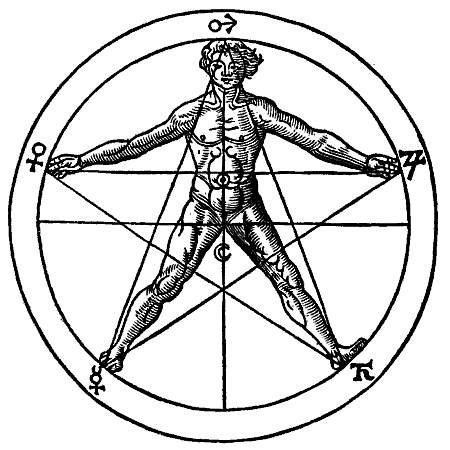
Pentogram with the body

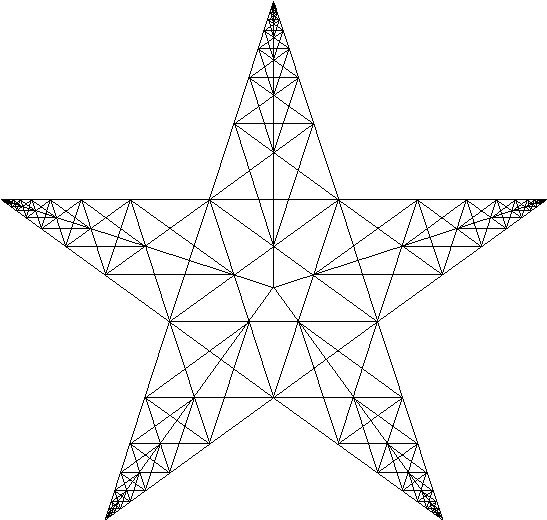
Star fractal

Digital art fractal

Computer generated Golden Mean fractal

Computer generated rainbow fractal

Fractal portal art

Computer generated star fractal

Golden mean spiral

Vortex sprirals created by fish

Black hole

Relationship between time and space

Platonic solids
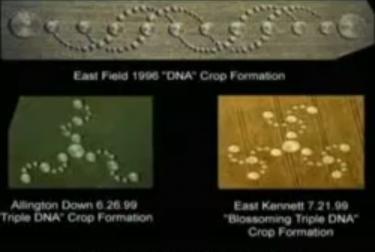
DNA
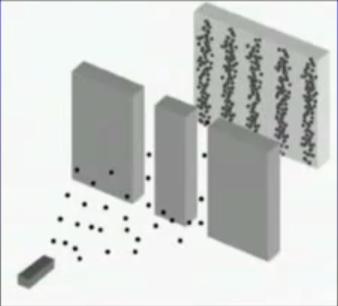
Double slit experiment with particles
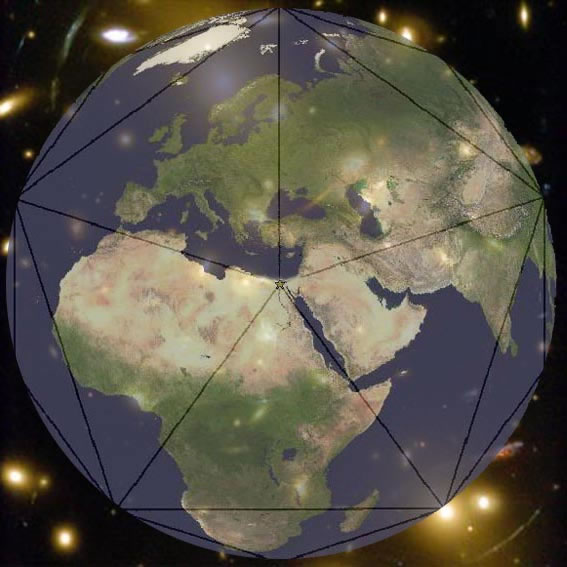
Pentagon on the Earth

VE sphere

3D flower of life

Petals
Solar System Planets Diameter |
- It is 12 light hours across. Since the speed of light is 300,000 km/second or 186,000 miles/second, 12 light hours is 12,960,000,000 kilometers, or 1.296 X 10 ^ 10, or 12 billion and 960 million kilometers, OR 8,052,970,651.4 miles.
- Diameter of the earth = 12 756.2 kilometers
- Diameter of Mercury = 4879 km at its equator
- The diameter of Mars is 6792 km at the equator and 6752 km at the poles. Mean Diameter = 6772 km.
- Venus Diameter: 12103.6 km (7700 miles) ...
- Diameter in jupiter 142800 km.
- Saturn's diameter is around 75000 miles 120000 kilometers .
- Diameter of Uranus is 51118 km
- Pluto's diameter as 2274 kilometers (1413 miles)
- 12.1 nm, which is enough for the membrane thickness plus a M13 virus diameter Bacteria measure from 0.2 – 0.3 microns in diameter
- Many of the spherical bacteria are about 1 micrometer in diameter
- Diameter of red blood cell 0.0076mm
- The average cell in our body is about 50 micrometers (0.05 mm) in diameter
- The diameter of human hair ranges from 17 to 181 µm. micrometer
- The dermis also varies in thickness depending on the location of the skin. It is .3 mm on the eyelid and 3.0 mm on the back.
- Whereas the thinnest walls, about 50 nm, are found in inner cell layers. |
Large and Small |
- 100 B galaxies visible
- 30% disc shaped galaxies like the milky way
- %60 ellipticals, smaller and larger than milky way, some with thousand of billions
of stars
- 10% irregular galaxies universe growing at 600 km per second, no center, 13
B years
- There are black holes millions of times more massive than the sun and shoot
out electromagnetic radiation
from quasars
* Farther light travels the longer the wave length
- 1/10,000 of a second after big bang subatomic stuff formed
- After 500,000 years electromagnetic radiation and matter went their separate
ways, 1,000 B degrees, photons
were particle verses anti particles pairs, this happened as universe cooled
for every billion anti protons
there were a B and 1 neutrons, these leftovers formed known universe. The rest
canceled each other out and are back ground photon radiation
- 4 minutes after time zero hydrogen and helium nuclei formed, (alpha particles)
5 - 300,000 after time zero the atoms formed, causing electromagnetic radiation
to move feeling through matter.
- Ultimately total energy of Universe is zero because it all cancels each other
out, the negative energy
is gravity causes kinetic energy of motion, these together first forever
- At 10(-43) seconds old universe was 10 (94) grams cm (3) and 10 (-33) cm across
- Universe doubled in size in 5 B years
- Force of gravity between 2 objects infinity apart is 1 by infinity squared
- 99% universe is dark matter, unaffected by all forces but gravity, photons,
wimps, spread out evenly in universe
unlike visible matter go through us at 100 k per second
- 45 BB molecules in CM (3) of air at 0 degrees Celsius
- PROTON vs. H-ATOM SIZE: The diameter of a single proton has been measured and is found to be 10^-15 meters. The diameter of a single hydrogen atom in its ground state is 10^-10 meters. So the RATIO of the size of the hydrogen atom to the size of the proton is 10^5.
- DNA molecules have a consistant width of about 2.5 nanometers
- The diameter of a C60 "buckyball" is about 10 Angstrom (1 nanometer).
- The diameter of an atom ranges from about 0.1 to 0.5 nanometer
- A proton has a diameter of approximately one-millionth of a nanometer
- Diameter of red blood cell is 0.0076mm
- The diameter of the nucleus is in the range of 1.6 fm (1.6 × 10−15 m) (for a proton in light hydrogen) to about 15 fm (for the heaviest atoms.
- Central part of an atom or nucleus, has a diameter of about 10-15m or 1.6 fm in ...
- Galaxy with a diameter of about 100000 light-years containing about 200 billion stars.
- In the model km m cm diameter of Sun 1400000 23 (ball) distance from Sun to ...
- Earth's Diameter at the Equator: 7926.28 miles (12756.1 km)
- The Sun's diameter is 1.4 million kilometers
- A light-year is about 9461000000000 km.
- Diameter of the moon = 3 474.8 kilometers |
Big Stars Diameter in Kilometers |
- 160K how high satellites are
- Meteors burn up 100K up at 100,000 Kph
- Moon 81 X smaller than earth, 15.5 CM AWAY
- Mercury - 58 M kilos 5000 K diameter solar system 4.6 B years old
- Mars - Half Earths size
- Saturn - 10X earths diameter
- Neptune - 30X as far from sun as earth
- Sun big beach ball 30 inches70 cm across and earth is 75 meters away the
size of a pea, mercury is 30M away the size of a pinhead jupiter is 400 Meters away size of a tennis ball uranus 10
Aussie cent coin 1.5 Km away pluto a speck 18 ks away.
- Sirius 2,335,000
- Vega 4,315,000
- Pollux 11,120,000
- Arcturus 22,101,000
- Super giants 100 - 200 X the suns diameter
- Aldebaran 59,770,000
- Rigel 97,300,000
- Deneb 201,550,000
- Pistol star 450,520,000
- Betelgeuse 903,500,000
- Antares 1,330,000,000
- W chepei 2,644,800,000
- Globular's 10s of thousand to over a million stars, can be thousands per cubic
light year
- Milky way galaxy 946,100,000,000,000,000 10 Billion stars in
milky way, olympic swimming pool with drops of water
- Galactic center 30K light years away
- If the galaxy was as big as Australia stars would be almost invisible specs
200m apart and the solar system
is 20 MM across
- Nebula, hundreds of light years in size |
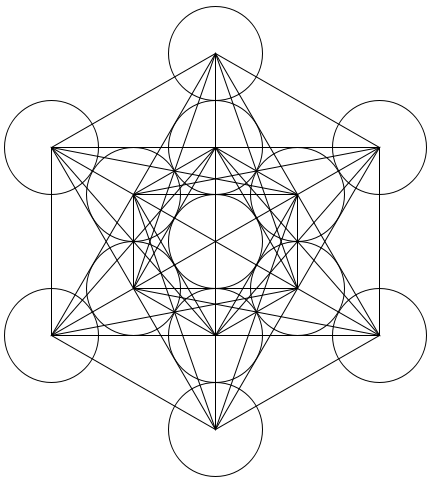
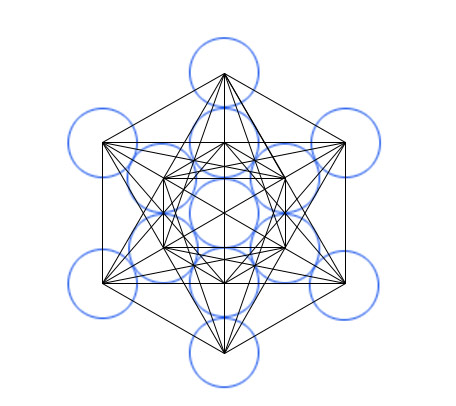
Metatrons Cube |
Gravity vs electromagnetisizm  |
Carl Swartzchild - the Swartzchild equation. Swartzchild singularity  |
Sacred geometry is geometry used in the design of sacred architecture and sacred art. The basic belief is that geometry and mathematical ratios, harmonics and proportion are also found in music, light, and cosmology. This value system has been found even in human prehistory and is considered by some to be a cultural universal of the human condition. Sacred geometry is foundational to the building of sacred structures such as temples, mosques, megaliths, monuments and churches; sacred spaces such as altars, temenoi and tabernacles; meeting places such as sacred groves, village greens and holy wells and the creation of religious art, iconography and using "divine" proportions. Sacred geometry-based arts may also be ephemeral, such as found in sandpainting and medicine wheels. |
As worldview |
|
Music  |
The discovery of the relationship of geometry and mathematics to music within the Classical Period is attributed to Pythagoras, who found that a string stopped halfway along its length produced an octave, while a ratio of 3/2 produced a fifth interval and 4/3 produced a fourth. Pythagoreans believed that this gave music powers of healing, as it could "harmonize" the out-of-balance body, and this belief has been revived in modern times]. Hans Jenny, a physician who pioneered the study of geometric figures formed by wave interactions and named that study cymatics, is often cited in this context. However, Dr. Jenny did not make healing claims for his work.
At least as late as Johannes Kepler (1571-1630), a belief in the geometric underpinnings of the cosmos persisted among scientists. Kepler explored the ratios of the planetary orbits, at first in two dimensions (having spotted that the ratio of the orbits of Jupiter and Saturn approximate to the in-circle and out-circle of an equilateral triangle). When this did not give him a neat enough outcome, he tried using the Platonic solids. In fact, planetary orbits can be related using two-dimensional geometric figures, but the figures do not occur in a particularly neat order. Even in his own lifetime (with less accurate data than we now possess) Kepler could see that the fit of the Platonic solids was imperfect, however, other geometric configurations are possible. |
Natural forms  |
Many forms observed in nature can be related to geometry (for sound reasons of resource optimization). For example, the chambered nautilus grows at a constant rate and so its shell forms a logarithmic spiral to accommodate that growth without changing shape. Also, honeybees construct hexagonal cells to hold their honey. These and other correspondences are seen by believers in sacred geometry to be further proof of the cosmic significance of geometric forms. But some scientists see such phenomena as the logical outcome of natural principles. |
Art and architecture  |
The golden ratio, geometric ratios, and geometric figures were often employed in the design of Egyptian, ancient Indian, Greek and Roman architecture. Medieval European cathedrals also incorporated symbolic geometry. Indian and Himalayan spiritual communities often constructed temples and fortifications on design plans of mandala and yantra. For examples of sacred geometry in art and architecture refer:
Contemporary usage
A contemporary usage of the term sacred geometry describes assertions of a mathematical order to the intrinsic nature of the universe. Scientists see the same geometric and mathematical patterns as arising directly from natural principles.
Among the most prevalent traditional geometric forms ascribed to sacred geometry are the sine wave, the sphere, the vesica piscis, the torus (donut), the 5 platonic solids, the golden spiral, the tesseract (4-dimensional cube), Fractals and the star tetrahedron (2 oppositely oriented and interpenetrating tetrahedrons) which leads to the merkaba.
The strands of our DNA, the cornea of our eye, snow flakes, pine cones, flower petals, diamond crystals, the branching of trees, a nautilus shell, the star we spin around, the galaxy we spiral within, the air we breathe, and all life forms as we know them emerge out of timeless geometric codes.
The designs of exalted holy places from the prehistoric monuments at Stonehenge and the Pyramid of Khufu at Giza, to the world's great cathedrals, mosques, and temples are based on these same principles of sacred geometry.
As far back as Greek Mystery schools 2500 years ago it was taught that there are five perfect 3-dimensional forms - the tetrahedron, hexahedron, octahedron, dodecahedron, and icosahedron...collectively known as the Platonic Solids; and that these form the foundation of everything in the physical world.
Modern scholars ridiculed this idea until the 1980's, when Professor Robert Moon at the University of Chicago demonstrated that the entire Periodic Table of Elements - literally everything in the physical world - truly is based on these same five geometric forms. In fact, throughout modern physics, chemistry, and biology, the sacred geometric patterns of creation are today being rediscovered.
The ancients knew that these patterns were codes symbolic of our own inner realm and that the experience of sacred geometry was essential to the education of the soul. Viewing and contemplating these forms can allow us to gaze directly at the face of deep wisdom and glimpse the inner workings of The Universal Mind.
LightSOURCE Arts is dedicated to bringing the power of sacred geometry and the wonderfully patterned beauty of Creation to your life.
Sacred Geometry Home Page by Bruce Rawles
In nature, we find patterns, designs and structures from the most minuscule particles, to expressions of life discernible by human eyes, to the greater cosmos. These inevitably follow geometrical archetypes, which reveal to us the nature of each form and its vibrational resonances. They are also symbolic of the underlying metaphysical principle of the inseparable relationship of the part to the whole. It is this principle of oneness underlying all geometry that permeates the architecture of all form in its myriad diversity. This principle of interconnectedness, inseparability and union provides us with a continuous reminder of our relationship to the whole, a blueprint for the mind to the sacred foundation of all things created. |
The Sphere  |
Starting with what may be the simplest and most perfect of forms, the sphere is an ultimate expression of unity, completeness, and integrity. There is no point of view given greater or lesser importance, and all points on the surface are equally accessible and regarded by the center from which all originate. Atoms, cells, seeds, planets, and globular star systems all echo the spherical paradigm of total inclusion, acceptance, simultaneous potential and fruition, the macrocosm and microcosm. |
The Circle  |
The circle is a two-dimensional shadow of the sphere which is regarded throughout cultural history as an icon of the ineffable oneness; the indivisible fulfillment of the Universe. All other symbols and geometries reflect various aspects of the profound and consummate perfection of the circle, sphere and other higher dimensional forms of these we might imagine.
The ratio of the circumference of a circle to its diameter, Pi, is the original transcendental and irrational number. (Pi equals about 3.14159265358979323846264338327950288419716939937511...) It cannot be expressed in terms of the ratio of two whole numbers, or in the language of sacred symbolism, the essence of the circle exists in a dimension that transcends the linear rationality that it contains. Our holistic perspectives, feelings and intuitions encompass the finite elements of the ideas that are within them, yet have a greater wisdom than can be expressed by those ideas alone. |
The Point  |
At the center of a circle or a sphere is always an infinitesimal point. The point needs no dimension, yet embraces all dimension. Transcendence of the illusions of time and space result in the point of here and now, our most primal light of consciousness. The proverbial "light at the end of the tunnel" is being validated by the ever-increasing literature on so-called "near-death experiences". If our essence is truly spiritual omnipresence, then perhaps the "point" of our being "here" is to recognize the oneness we share, validating all "individuals" as equally precious and sacred aspects of that one.
Life itself as we know it is inextricably interwoven with geometric forms, from the angles of atomic bonds in the molecules of the amino acids, to the helical spirals of DNA, to the spherical prototype of the cell, to the first few cells of an organism which assume vesical, tetrahedral, and star (double) tetrahedral forms prior to the diversification of tissues for different physiological functions. Our human bodies on this planet all developed with a common geometric progression from one to two to four to eight primal cells and beyond.
Almost everywhere we look, the mineral intelligence embodied within crystalline structures follows a geometry unfaltering in its exactitude. The lattice patterns of crystals all express the principles of mathematical perfection and repetition of a fundamental essence, each with a characteristic spectrum of resonances defined by the angles, lengths and relational orientations of its atomic components. |
The Square Root of Two  |
The square root of 2 embodies a profound principle of the whole being more than the sum of its parts. (The square root of two equals about 1.414213562...) The orthogonal dimensions (axes at right angles) form the conjugal union of the horizontal and vertical which give birth to the greater offspring of the hypotenuse. The new generation possesses the capacity for synthesis, growth, integration and reconciliation of polarities by spanning both perspectives equally. The root of two originating from the square leads to a greater unity, a higher expression of its essential truth, faithful to its lineage.
The fact that the root is irrational expresses the concept that our higher dimensional faculties can't always necessarily be expressed in lower order dimensional terms - e.g. "And the light shineth in darkness; and the darkness comprehended it not." (from the Gospel of St. John, Chapter 1, verse 5). By the same token, we have the capacity to surpass the genetically programmed limitations of our ancestors, if we can shift into a new frame of reference (i.e. neutral with respect to prior axes, yet formed from that matrix-seed conjugation. Our dictionary refers to the word matrix both as a womb and an array (or grid lattice). Our language has some wonderful built-in metaphors if we look for them! |
The Golden Ratio  |
The golden ratio (a.k.a. phi ratio a.k.a. sacred cut a.k.a. golden mean a.k.a. divine proportion) is another fundamental measure that seems to crop up almost everywhere, including crops. (The golden ratio is about 1.618033988749894848204586834365638117720309180...) The golden ratio is the unique ratio such that the ratio of the whole to the larger portion is the same as the ratio of the larger portion to the smaller portion. As such, it symbolically links each new generation to its ancestors, preserving the continuity of relationship as the means for retracing its lineage.
The golden ratio (phi) has some unique properties and makes some interesting appearances: |
- phi = phi^2 - 1; therefore 1 + phi = phi^2; phi + phi^2 = phi^3; phi^2 + - phi^3= phi^4; ad infinitum. phi = (1 + square root(5)) / 2 from quadratic formula, 1 + phi = phi^2. phi = 1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/...))))) phi = 1 + square root(1 + square root(1 + square root(1 + square root(1 + square root(1 + ...)))))
- phi = (sec 72)/2 =(csc 18)/2 = 1/(2 cos 72) = 1/(2 sin 18) = 2 sin 54 = 2 cos 36 = 2/(csc 54) = 2/ (sec 36) for all you trigonometry enthusiasts.
- phi = the ratio of segments in a 5-pointed star (pentagram) considered sacred to Plato and Pythagoras in their mystery schools. Note that each larger (or smaller) section is related by the phi ratio, so that a power series of the golden ratio raised to successively higher (or lower) powers is automatically generated: phi, phi^2, phi^3, phi^4, phi^5, etc. phi = apothem to bisected base ratio in the Great Pyramid of Giza phi = ratio of adjacent terms of the famous Fibonacci Series evaluated at infinity; the Fibonacci Series is a rather ubiquitous set of numbers that begins with one and one and each term thereafter is the sum of the prior two terms, thus: 1,1,2,3,5,8,13,21,34,55,89,144... (interesting that the 12th term is 12 "raised to a higher power", which appears prominently in a vast collection of metaphysical literature) |
| The mathematician credited with the discovery of this series is Leonardo Pisano Fibonacci and there is a publication devoted to disseminating information about its unique mathematical properties, The Fibonacci Quarterly
Fibonacci ratios appear in the ratio of the number of spiral arms in daisies, in the chronology of rabbit populations, in the sequence of leaf patterns as they twist around a branch, and a myriad of places in nature where self-generating patterns are in effect. The sequence is the rational progression towards the irrational number embodied in the quintessential golden ratio.
This most aesthetically pleasing proportion, phi, has been utilized by numerous artists since (and probably before!) the construction of the Great Pyramid. As scholars and artists of eras gone by discovered (such as Leonardo da Vinci, Plato, and Pythagoras), the intentional use of these natural proportions in art of various forms expands our sense of beauty, balance and harmony to optimal effect. Leonardo da Vinci used the Golden Ratio in his painting of The Last Supper in both the overall composition (three vertical Golden Rectangles, and a decagon (which contains the golden ratio) for alignment of the central figure of Jesus.
The outline of the Parthenon at the Acropolis near Athens, Greece is enclosed by a Golden Rectangle by design.
The Square Root of 3 and the Vesica Piscis
The Vesica Piscis is formed by the intersection of two circles or spheres whose centers exactly touch. This symbolic intersection represents the "common ground", "shared vision" or "mutual understanding" between equal individuals. The shape of the human eye itself is a Vesica Piscis. The spiritual significance of "seeing eye to eye" to the "mirror of the soul" was highly regarded by numerous Renaissance artists who used this form extensively in art and architecture. The ratio of the axes of the form is the square root of 3, which alludes to the deepest nature of the triune which cannot be adequately expressed by rational language alone. |
Spirals |
This spiral generated by a recursive nest of Golden Triangles (triangles with relative side lengths of 1, phi and phi) is the classic shape of the Chambered Nautilus shell. The creature building this shell uses the same proportions for each expanded chamber that is added; growth follows a law which is everywhere the same. The outer triangle is the same as one of the five "arms" of the pentagonal graphic above. |
Toroids |
Rotating a circle about a line tangent to it creates a torus, which is similar to a donut shape where the center exactly touches all the "rotated circles." The surface of the torus can be covered with 7 distinct areas, all of which touch each other; an example of the classic "map problem" where one tries to find a map where the least number of unique colors are needed. In this 3-dimensional case, 7 colors are needed, meaning that the torus has a high degree of "communication" across its surface. The image shown is a "birds-eye" view. |
Dimensionality |
The progression from point (0-dimensional) to line (1-dimensional) to plane (2-dimensional) to space (3-dimensional) and beyond leads us to the question - if mapping from higher order dimensions to lower ones loses vital information (as we can readily observe with optical illusions resulting from third to second dimensional mapping), does our "fixation" with a 3-dimensional space introduce crucial distortions in our view of reality that a higher-dimensional perspective would not lead us to? |
Fractals and Recursive Geometries |
There is a wealth of good literature on this subject; it's always fascinating how nature propagates the same essence regardless of the magnitude of its expression...our spirit is spaceless yet can manifest aspects of its individuality at any scale. |
Perfect Right Triangles |
The 3/4/5, 5/12/13 and 7/24/25 triangles are examples of right triangles whose sides are whole numbers. The graphic above contains several of each of these triangles. The 3/4/5 triangle is contained within the so-called "King's Chamber" of the Great Pyramid, along with the 2/3/root5 and 5/root5/2root5 triangles, utilizing the various diagonals and sides. |
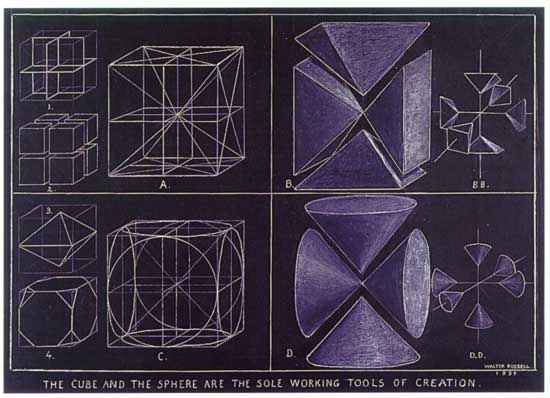
The Platonic Solids |
The 5 Platonic solids (Tetrahedron, Cube or (Hexahedron), Octahedron, Dodecahedron and Icosahedron) are ideal, primal models of crystal patterns that occur throughout the world of minerals in countless variations. These are the only five regular polyhedra, that is, the only five solids made from the same equilateral, equiangular polygons. To the Greeks, these solids symbolized fire, earth, air, spirit (or ether) and water respectively. The cube and octahedron are duals, meaning that one can be created by connecting the midpoints of the faces of the other. The icosahedron and dodecahedron are also duals of each other, and three mutually perpendicular, mutually bisecting golden rectangles can be drawn connecting their vertices and midpoints, respectively. The tetrahedron is a dual to itself. |
The Archimedean Solids |
There are 13 Archimedean solids, each of which are composed of two or more different regular polygons. Interestingly, 5 (Platonic) and 13 (Archimedean) are both Fibonacci numbers, and 5, 12 and 13 form a perfect right triangle. |
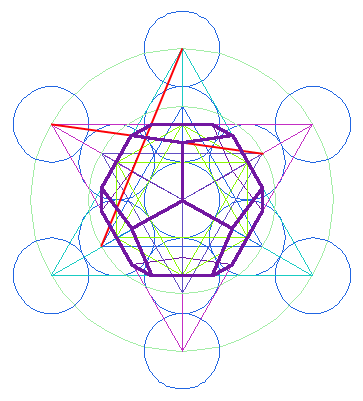
Metatron's Cube |
Metatron's Cube contains 2-dimensional images of the Platonic Solids (as shown above) and many other primal forms. |
The Flower of Life |
Indelibly etched on the walls of temple of the Osirion at Abydos, Egypt, the Flower of Life contains a vast Akashic system of information, including templates for the five Platonic Solids. The background graphic for this page is a repetitive hexagonal grid based on the Flower of Life. |
Gravitational singularity |
A gravitational singularity or spacetime singularity is a location where the quantities that are used to measure the gravitational field become infinite in a way that does not depend on the coordinate system. These quantities are the scalar invariant curvatures of spacetime, some of which are a measure of the density of matter.
For the purposes of proving the Penrose-Hawking singularity theorems, a spacetime with a singularity is defined to be one that contains geodesics that cannot be extended in a smooth manner. The end of such a geodesic is considered to be the singularity. This is a different definition, useful for proving theorems.
The two most important types of spacetime singularities are curvature singularities and conical singularities. Singularities can also be divided according to whether they are covered by an event horizon or not (naked singularities). According to general relativity, the initial state of the universe, at the beginning of the Big Bang, was a singularity. Another type of singularity predicted by general relativity is inside a black hole: any star collapsing beyond a certain point would form a black hole, inside which a singularity (covered by an event horizon) would be formed, as all the matter would flow into a certain point (or a circular line, if the black hole is rotating). These singularities are also known as curvature singularities. |
Interpretation  |
Many theories in physics have mathematical singularities of one kind or another. Equations for these physical theories predict that the rate of change of some quantity becomes infinite or increases without limit. This is generally a sign for a missing piece in the theory, as in the Ultraviolet Catastrophe and in renormalization.
In supersymmetry, a singularity in the moduli space happens usually when there are additional massless degrees of freedom in that certain point. Similarly, it is thought that singularities in spacetime often mean that there are additional degrees of freedom that exist only within the vicinity of the singularity. The same fields related to the whole spacetime, also exist; for example, the electromagnetic field. In known examples of string theory, the latter degrees of freedom are related to closed strings, while the degrees of freedom are "stuck" to the singularity and related either to open strings or to the twisted sector of an orbifold.
Some theories, such as the theory of Loop quantum gravity suggest that singularities may not exist. The idea is that due to quantum gravity effects, there is a minimum distance beyond which the force of gravity no longer continue to increase as the distance between the masses become shorter. |
Types  |
Curvature  |
Solutions to the equations of general relativity or another theory of gravity (such as supergravity), often result in encountering points where the metric blows up to infinity. However, many of these points are in fact completely regular. Moreover, the infinities are merely a result of using an inappropriate coordinate system at this point. Thus, in order to test whether there is a singularity at a certain point, one must check whether at this point diffeomorphism invariant quantities (i.e. scalars) become infinite. Such quantities are the same in every coordinate system, so these infinities will not "go away" by a change of coordinates.
An example is the Schwarzschild solution that describes a non-rotating, uncharged black hole. In coordinate systems convenient for working in regions far away from the black hole, a part of the metric becomes infinite at the event horizon. However, spacetime at the event horizon is regular. The regularity becomes evident when changing to another coordinate system (such as the Kruskal coordinates), where the metric is perfectly smooth. On the other hand, in the center of the black hole, where the metric becomes infinite as well, the solutions suggest singularity exists. The existence of the singularity can be verified by noting that the Kretschmann scalar or square of the Riemann tensor, RμνρσRμνρσ, which is diffeomorphism invariant, is infinite. While in a non-rotating black hole the singularity occurs at a single point in the model coordinates, called a "point singularity", in a rotating black hole, also known as a Kerr black hole, the singularity occurs on a ring (a circular line), defined as a "ring singularity". Such a singularity may also theoretically become a wormhole.[1]
More generally, a spacetime is considered singular if it is geodesically incomplete, meaning that there are freely-falling particles whose motion cannot be determined at a finite time at the point of reaching the singularity. For example, any observer below the event horizon of a nonrotating black hole would fall into its center within a finite period of time. The simplest Big Bang cosmological model of the universe contains a causal singularity at the start of time (t=0), where all timelike geodesics have no extensions into the past. Extrapolating backward to this hypothetical time 0 results in a universe of size 0 in all spatial dimensions, infinite density, infinite temperature, and infinite space-time curvature. |
Conical  |
A conical singularity occurs when there is a point where the limit of every diffeomorphism invariant quantity is finite. In which case, spacetime is not smooth at the point of the limit itself. Thus, spacetime looks like a cone around this point, where the singularity is located at the tip of the cone. The metric can be finite everywhere if a suitable coordinate system is used.
An example of such a conical singularity is a cosmic string. |
Naked  |
Until the early 1990s, it was widely believed that general relativity hides every singularity behind an event horizon, making naked singularities impossible. This is referred to as the cosmic censorship hypothesis. However, in 1991 Shapiro and Teukolsky performed computer simulations of a rotating plane of dust that indicated that general relativity might allow for "naked" singularities. What these objects would actually look like in such a model is unknown. Nor is it known whether singularities would still arise if the simplifying assumptions used to make the simulation were removed. |
Entropy  |
Before Stephen Hawking came up with the concept of Hawking radiation, the question of black holes having entropy was avoided. However, this concept demonstrates that black holes can radiate energy, which conserves entropy and solves the incompatibility problems with the second law of thermodynamics. Entropy, however, implies heat and therefore temperature. The loss of energy also suggests that black holes do not last forever, but rather "evaporate" slowly. Small black holes tend to be hotter whereas larger ones tend to be colder. All known black holes are so large that their temperature is far below that of the cosmic background radiation, so they are all gaining energy. They will not begin to lose energy until a cosmological redshift of more than a million is reached, rather than the thousand or so since the background radiation formed. |
Unified field theory  |
This article describes unified field theory as it is currently understood in connection with quantum theory. Earlier attempts based on classical physics are described in the article on classical unified field theories.
There may be no a priori reason why the correct description of nature has to be a unified field theory; however, this goal has led to a great deal of progress in modern theoretical physics and continues to motivate research. Unified field theory is only one possible approach to unification of physics.
|
Introduction  |
According to the current understanding of physics, forces between objects (e.g. gravitation) are not transmitted directly between the two objects, but instead go through intermediary entities called fields. All four of the known fundamental forces are mediated by fields, which in the Standard Model of particle physics result from exchange of bosons (integral- spin particles). Specifically the four interactions to be unified are (from strongest to weakest):
|
History  |
The first successful (classical) unified field theory was developed by James Clerk Maxwell. In 1820 Hans Christian Ørsted discovered that electric currents exerted forces on magnets, while in 1831, Michael Faraday made the observation that time-varying magnetic fields could induce electric currents. Until then, electricity and magnetism had been thought of as unrelated phenomena. In 1864, Maxwell published his famous paper on a dynamical theory of the electromagnetic field. This was the first example of a theory that was able to encompass previous separate field theories (namely electricity and magnetism) to provide a unifying theory of electromagnetism. Later, in his theory of special relativity Albert Einstein was able to explain the unity of electricity and magnetism as a consequence of the unification of space and time into an entity we now call spacetime.
In 1921 Theodor Kaluza extended General Relativity to five dimensions and in 1926 Oscar Klein proposed that the fourth spatial dimension be curled up (or compactified) into a small, unobserved circle. This was dubbed Kaluza-Klein theory. It was quickly noticed that this extra spatial direction gave rise to an additional force similar to electricity and magnetism. This was pursued as the basis for some of Albert Einstein's later unsuccessful attempts at a unified field theory. Einstein and others pursued various non-quantum approaches to unifying these forces; however as quantum theory became generally accepted as fundamental, most physicists came to view all such theories as doomed to failure. |
Modern progress  |
In 1963 American physicist Sheldon Glashow proposed that the weak nuclear force and electricity and magnetism could arise from a partially unified electroweak theory. In 1967, Pakistani Abdus Salam and American Steven Weinberg independently revised Glashow's theory by having the masses for the W particle and Z particle arise through spontaneous symmetry breaking with the Higgs mechanism. This unified theory was governed by the exchange of four particles: the photon for electromagnetic interactions, a neutral Z particle and two charged W particles for weak interaction. As a result of the spontaneous symmetry breaking, the weak force becomes short range and the Z and W bosons acquire masses of 80.4 and 91.2 GeV / c2, respectively. Their theory was first given experimental support by the discovery of weak neutral currents in 1973. In 1983, the Z and W bosons were first produced at CERN by Carlo Rubbia's team. For their insights, Salam, Glashow and Weinberg were awarded the Nobel Prize in Physics in 1979. Carlo Rubbia and Simon van der Meer received the Prize in 1984.
After Gerardus 't Hooft showed the Glashow-Weinberg-Salam electroweak interactions was mathematically consistent, the electroweak theory became a template for further attempts at unifying forces. In 1974, Sheldon Glashow and Howard Georgi proposed unifying the strong and electroweak interactions into Georgi-Glashow model, the first Grand Unified Theory, which would have observable effects for energies much above 100 GeV.
Since then there have been several proposals for Grand Unified Theories, e.g. the Pati-Salam model, although none is currently universally accepted. A major problem for experimental tests of such theories is the energy scale involved, which is well beyond the reach of current accelerators. Grand Unified Theories make predictions for the relative strengths of the strong, weak, and electromagnetic forces, and in 1991 LEP determined that supersymmetric theories have the correct ratio of couplings for a Georgi-Glashow Grand Unified Theory. Many Grand Unified Theories (but not Pati-Salam) predict that the proton can decay, and if this were to be seen, details of the decay products could give hints at more aspects of the Grand Unified Theory. It is at present unknown if the proton can decay, although experiments have determined a lower bound of 1035 years for its lifetime. |
Current status  |
|
Non-mainstream theories  |
Albert Einstein famously spent the last two decades of his life searching for a Unified Field Theory. This has led to a great deal of fascination with the subject and has drawn many people from outside the mainstream of the physics community to work on such a theory. Most of this work typically appears in non-peer reviewed sources, such as self-published books or personal websites. The work that appears outside of the standard scientific channels may or may not be considered pseudoscience by definition.
Examples of "non-mainstream" theories are Heim theory and Antony Garrett Lisi's "An Exceptionally Simple Theory of Everything."
|
Quantum mechanics |
Quantum mechanics (QM) is a set of scientific principles describing the known behavior of energy and matter that predominate at the atomic scale. QM gets its name from the notion of quantum, and the quantum value is the Planck constant. The wave–particle duality of energy and matter at the atomic scale provides a unified view of the behavior of particles such as photons and electrons. While the notion of the photon as a quantum of light energy is commonly understood as a particle of light that has an energy value governed by the Planck constant, what is quantized for an electron is the angular momentum it can have as it is bound in an atomic orbital. When not bound to an atom, an electron's energy is no longer quantized, but it displays, like any other massy particle, a Compton wavelength. While a photon does not have mass, it does have linear momentum. The full significance of the Planck constant is expressed in physics through the abstract mathematical notion of action.
The mathematical formulation of quantum mechanics is abstract and its implications are often non-intuitive. The centerpiece of this mathematical system is the wavefunction. The wavefunction is a mathematical function of time and space that can provide information about the position and momentum of a particle, but only as probabilities, as dictated by the constraints imposed by the uncertainty principle. Mathematical manipulations of the wavefunction usually involve the bra-ket notation, which requires an understanding of complex numbers and linear functionals. Many of the results of QM can only be expressed mathematically and do not have models that are as easy to visualize as those of classical mechanics. For instance, the ground state in quantum mechanical model is a non-zero energy state that is the lowest permitted energy state of a system, rather than a more traditional system that is thought of as simple being at rest with zero kinetic energy.
Overview
The word quantum is Latin for "how great" or "how much." In quantum mechanics, it refers to a discrete unit that quantum theory assigns to certain physical quantities, such as the energy of an atom at rest (see Figure 1, at right). The discovery that particles are discrete packets of energy with wave-like properties led to the branch of physics that deals with atomic and subatomic systems which is today called quantum mechanics. It is the underlying mathematical framework of many fields of physics, including condensed matter physics, solid-state physics, atomic physics, molecular physics, computational chemistry, quantum chemistry, particle physics, and nuclear physics. The foundations of quantum mechanics were established during the first half of the twentieth century by Werner Heisenberg, Max Planck, Louis de Broglie, Albert Einstein, Niels Bohr, Erwin Schrödinger, Max Born, John von Neumann, Paul Dirac, Wolfgang Pauli, David Hilbert, and others. Some fundamental aspects of the theory are still actively studied.
Quantum mechanics is essential to understand the behavior of systems at atomic length scales and smaller. For example, if classical mechanics governed the workings of an atom, electrons would rapidly travel towards and collide with the nucleus, making stable atoms impossible. However, in the natural world the electrons normally remain in an uncertain, non-deterministic "smeared" (wave-particle wave function) orbital path around or "through" the nucleus, defying classical electromagnetism.
Quantum mechanics was initially developed to provide a better explanation of the atom, especially the spectra of light emitted by different atomic species. The quantum theory of the atom was developed as an explanation for the electron's staying in its orbital, which could not be explained by Newton's laws of motion and by Maxwell's laws of classical electromagnetism.
In the formalism of quantum mechanics, the state of a system at a given time is described by a complex wave function (sometimes referred to as orbitals in the case of atomic electrons), and more generally, elements of a complex vector space. This abstract mathematical object allows for the calculation of probabilities of outcomes of concrete experiments. For example, it allows one to compute the probability of finding an electron in a particular region around the nucleus at a particular time. Contrary to classical mechanics, one can never make simultaneous predictions of conjugate variables, such as position and momentum, with accuracy. For instance, electrons may be considered to be located somewhere within a region of space, but with their exact positions being unknown. Contours of constant probability, often referred to as “clouds,” may be drawn around the nucleus of an atom to conceptualize where the electron might be located with the most probability. Heisenberg's uncertainty principle quantifies the inability to precisely locate the particle given its conjugate.
The other exemplar that led to quantum mechanics was the study of electromagnetic waves such as light. When it was found in 1900 by Max Planck that the energy of waves could be described as consisting of small packets or quanta, Albert Einstein further developed this idea to show that an electromagnetic wave such as light could be described by a particle called the photon with a discrete energy dependent on its frequency. This led to a theory of unity between subatomic particles and electromagnetic waves called wave–particle duality in which particles and waves were neither one nor the other, but had certain properties of both. While quantum mechanics describes the world of the very small, it also is needed to explain certain “macroscopic quantum systems” such as superconductors and superfluids.
Broadly speaking, quantum mechanics incorporates four classes of phenomena that classical physics cannot account for: (I) the quantization (discretization) of certain physical quantities, (II) wave-particle duality, (III) the uncertainty principle, and (IV) quantum entanglement. Each of these phenomena is described in detail in subsequent sections.
|
History  |
The history of quantum mechanics[7] began essentially with the 1838 discovery of cathode rays by Michael Faraday, the 1859 statement of the black body radiation problem by Gustav Kirchhoff, the 1877 suggestion by Ludwig Boltzmann that the energy states of a physical system could be discrete, and the 1900 quantum hypothesis by Max Planck that any energy is radiated and absorbed in quantities divisible by discrete "energy elements," E, such that each of these energy elements is proportional to the frequency ν with which they each individually radiate energy, as defined by the following formula: where h is Planck's action constant. Planck insisted[8] that this was simply an aspect of the processes of absorption and emission of radiation and had nothing to do with the physical reality of the radiation itself. However, at that time, this appeared not to explain the photoelectric effect (1839), i.e. that shining light on certain materials can function to eject electrons from the material. In 1905, basing his work on Planck’s quantum hypothesis, Albert Einstein[9] postulated that light itself consists of individual quanta.
In the mid-1920s, developments in quantum mechanics quickly led to it becoming the standard formulation for atomic physics. In the summer of 1925, Bohr and Heisenberg published results that closed the "Old Quantum Theory". Light quanta came to be called photons (1926). From Einstein's simple postulation was born a flurry of debating, theorizing and testing, and thus, the entire field of quantum physics, leading to its wider acceptance at the 1927 5th Solvay Conference. |
Quantum mechanics and classical physics  |
Predictions of quantum mechanics have been verified experimentally to a very high degree of accuracy. Thus, the current logic of correspondence principle between classical and quantum mechanics is that all objects obey laws of quantum mechanics, and classical mechanics is just a quantum mechanics of large systems (or a statistical quantum mechanics of a large collection of particles). Laws of classical mechanics thus follow from laws of quantum mechanics at the limit of large systems or large quantum numbers.[10] However, chaotic systems do not have good quantum numbers, and quantum chaos studies the relationship between classical and quantum descriptions in these systems.
The main differences between classical and quantum theories have already been mentioned above in the remarks on the Einstein-Podolsky-Rosen paradox. Essentially the difference boils down to the statement that quantum mechanics is coherent (addition of amplitudes), whereas classical theories are incoherent (addition of intensities). Thus, such quantities as coherence lengths and coherence times come into play. For microscopic bodies the extension of the system is certainly much smaller than the coherence length; for macroscopic bodies one expects that it should be the other way round. An exception to this rule can occur at extremely low temperatures, when quantum behavior can manifest itself on more "macroscopic" scales (see Bose-Einstein condensate).
This is in accordance with the following observations:
Many “macroscopic” properties of “classic” systems are direct consequences of quantum behavior of its parts. For example, stability of bulk matter (which consists of atoms and molecules which would quickly collapse under electric forces alone), rigidity of this matter, mechanical, thermal, chemical, optical and magnetic properties of this matter—they are all results of interaction of electric charges under the rules of quantum mechanics.
While the seemingly exotic behavior of matter posited by quantum mechanics and relativity theory become more apparent when dealing with extremely fast-moving or extremely tiny particles, the laws of classical “Newtonian” physics still remain accurate in predicting the behavior of surrounding (“large”) objects—of the order of the size of large molecules and bigger—at velocities much smaller than the velocity of light. |
Theory  |
There are numerous mathematically equivalent formulations of quantum mechanics. One of the oldest and most commonly used formulations is the transformation theory proposed by Cambridge theoretical physicist Paul Dirac, which unifies and generalizes the two earliest formulations of quantum mechanics, matrix mechanics (invented by Werner Heisenberg) and wave mechanics (invented by Erwin Schrödinger).
In this formulation, the instantaneous state of a quantum system encodes the probabilities of its measurable properties, or "observables". Examples of observables include energy, position, momentum, and angular momentum. Observables can be either continuous (e.g., the position of a particle) or discrete (e.g., the energy of an electron bound to a hydrogen atom).
Generally, quantum mechanics does not assign definite values to observables. Instead, it makes predictions using probability distributions; that is, the probability of obtaining possible outcomes from measuring an observable. Oftentimes these results are skewed by many causes, such as dense probability clouds[18] or quantum state nuclear attraction. Naturally, these probabilities will depend on the quantum state at the "instant" of the measurement. Hence, uncertainty is involved in the value. There are, however, certain states that are associated with a definite value of a particular observable. These are known as "eigenstates" of the observable ("eigen" can be roughly translated from German as inherent or as a characteristic[21]). In the everyday world, it is natural and intuitive to think of everything (every observable) as being in an eigenstate. Everything appears to have a definite position, a definite momentum, a definite energy, and a definite time of occurrence. However, quantum mechanics does not pinpoint the exact values of a particle for its position and momentum (since they are conjugate pairs) or its energy and time (since they too are conjugate pairs); rather, it only provides a range of probabilities of where that particle might be given its momentum and momentum probability. Therefore, it is helpful to use different words to describe states having uncertain values and states having definite values (eigenstate).
For example, consider a free particle. In quantum mechanics, there is wave-particle duality so the properties of the particle can be described as the properties of a wave. Therefore, its quantum state can be represented as a wave of arbitrary shape and extending over space as a wave function. The position and momentum of the particle are observables. The Uncertainty Principle states that both the position and the momentum cannot simultaneously be measured with full precision at the same time. However, one can measure the position alone of a moving free particle creating an eigenstate of position with a wavefunction that is very large (a Dirac delta) at a particular position x and zero everywhere else. If one performs a position measurement on such a wavefunction, the result x will be obtained with 100% probability (full certainty). This is called an eigenstate of position (mathematically more precise: a generalized position eigenstate (eigendistribution)). If the particle is in an eigenstate of position then its momentum is completely unknown. On the other hand, if the particle is in an eigenstate of momentum then its position is completely unknown. In an eigenstate of momentum having a plane wave form, it can be shown that the wavelength is equal to h/p, where h is Planck's constant and p is the momentum of the eigenstate.
Usually, a system will not be in an eigenstate of the observable we are interested in. However, if one measures the observable, the wavefunction will instantaneously be an eigenstate (or generalized eigenstate) of that observable. This process is known as wavefunction collapse, a debatable process. It involves expanding the system under study to include the measurement device. If one knows the corresponding wave function at the instant before the measurement, one will be able to compute the probability of collapsing into each of the possible eigenstates. For example, the free particle in the previous example will usually have a wavefunction that is a wave packet centered around some mean position x0, neither an eigenstate of position nor of momentum. When one measures the position of the particle, it is impossible to predict with certainty the result. It is probable, but not certain, that it will be near x0, where the amplitude of the wave function is large. After the measurement is performed, having obtained some result x, the wave function collapses into a position eigenstate centered at x.
Wave functions can change as time progresses. An equation known as the Schrödinger equation describes how wave functions change in time, a role similar to Newton's second law in classical mechanics. The Schrödinger equation, applied to the aforementioned example of the free particle, predicts that the center of a wave packet will move through space at a constant velocity, like a classical particle with no forces acting on it. However, the wave packet will also spread out as time progresses, which means that the position becomes more uncertain. This also has the effect of turning position eigenstates (which can be thought of as infinitely sharp wave packets) into broadened wave packets that are no longer position eigenstates.[27] Some wave functions produce probability distributions that are constant or independent of time, such as when in a stationary state of constant energy, time drops out of the absolute square of the wave function. Many systems that are treated dynamically in classical mechanics are described by such "static" wave functions. For example, a single electron in an unexcited atom is pictured classically as a particle moving in a circular trajectory around the atomic nucleus, whereas in quantum mechanics it is described by a static, spherically symmetric wavefunction surrounding the nucleus . (Note that only the lowest angular momentum states, labeled s, are spherically symmetric).
The time evolution of wave functions is deterministic in the sense that, given a wavefunction at an initial time, it makes a definite prediction of what the wavefunction will be at any later time. During a measurement, the change of the wavefunction into another one is not deterministic, but rather unpredictable, i.e., random. A time-evolution simulation can be seen here.
The probabilistic nature of quantum mechanics thus stems from the act of measurement. This is one of the most difficult aspects of quantum systems to understand. It was the central topic in the famous Bohr-Einstein debates, in which the two scientists attempted to clarify these fundamental principles by way of thought experiments. In the decades after the formulation of quantum mechanics, the question of what constitutes a "measurement" has been extensively studied. Interpretations of quantum mechanics have been formulated to do away with the concept of "wavefunction collapse"; see, for example, the relative state interpretation. The basic idea is that when a quantum system interacts with a measuring apparatus, their respective wavefunctions become entangled, so that the original quantum system ceases to exist as an independent entity. For details, see the article on measurement in quantum mechanics. |
Mathematical formulation  |
In the mathematically rigorous formulation of quantum mechanics, developed by Paul Dirac[31] and John von Neumann, the possible states of a quantum mechanical system are represented by unit vectors (called "state vectors") residing in a complex separable Hilbert space (variously called the "state space" or the "associated Hilbert space" of the system) well defined up to a complex number of norm 1 (the phase factor). In other words, the possible states are points in the projectivization of a Hilbert space, usually called the complex projective space. The exact nature of this Hilbert space is dependent on the system; for example, the state space for position and momentum states is the space of square-integrable functions, while the state space for the spin of a single proton is just the product of two complex planes. Each observable is represented by a maximally-Hermitian (precisely: by a self-adjoint) linear operator acting on the state space. Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate. If the operator's spectrum is discrete, the observable can only attain those discrete eigenvalues.
The time evolution of a quantum state is described by the Schrödinger equation, in which the Hamiltonian, the operator corresponding to the total energy of the system, generates time evolution.
The inner product between two state vectors is a complex number known as a probability amplitude. During a measurement, the probability that a system collapses from a given initial state to a particular eigenstate is given by the square of the absolute value of the probability amplitudes between the initial and final states. The possible results of a measurement are the eigenvalues of the operator - which explains the choice of Hermitian operators, for which all the eigenvalues are real. We can find the probability distribution of an observable in a given state by computing the spectral decomposition of the corresponding operator. Heisenberg's uncertainty principle is represented by the statement that the operators corresponding to certain observables do not commute.
The Schrödinger equation acts on the entire probability amplitude, not merely its absolute value. Whereas the absolute value of the probability amplitude encodes information about probabilities, its phase encodes information about the interference between quantum states. This gives rise to the wave-like behavior of quantum states.
It turns out that analytic solutions of Schrödinger's equation are only available for a small number of model Hamiltonians, of which the quantum harmonic oscillator, the particle in a box, the hydrogen molecular ion and the hydrogen atom are the most important representatives. Even the helium atom, which contains just one more electron than hydrogen, defies all attempts at a fully analytic treatment. There exist several techniques for generating approximate solutions. For instance, in the method known as perturbation theory one uses the analytic results for a simple quantum mechanical model to generate results for a more complicated model related to the simple model by, for example, the addition of a weak potential energy. Another method is the "semi-classical equation of motion" approach, which applies to systems for which quantum mechanics produces weak deviations from classical behavior. The deviations can be calculated based on the classical motion. This approach is important for the field of quantum chaos.
An alternative formulation of quantum mechanics is Feynman's path integral formulation, in which a quantum-mechanical amplitude is considered as a sum over histories between initial and final states; this is the quantum-mechanical counterpart of action principles in classical mechanics.
|
Interactions with other scientific theories  |
The fundamental rules of quantum mechanics are very deep. They assert that the state space of a system is a Hilbert space and the observables are Hermitian operators acting on that space, but do not tell us which Hilbert space or which operators, or if it even exists. These must be chosen appropriately in order to obtain a quantitative description of a quantum system. An important guide for making these choices is the correspondence principle, which states that the predictions of quantum mechanics reduce to those of classical physics when a system moves to higher energies or equivalently, larger quantum numbers. In other words, classic mechanics is simply a quantum mechanics of large systems. This "high energy" limit is known as the classical or correspondence limit. One can therefore start from an established classical model of a particular system, and attempt to guess the underlying quantum model that gives rise to the classical model in the correspondence limit.
When quantum mechanics was originally formulated, it was applied to models whose correspondence limit was non-relativistic classical mechanics. For instance, the well-known model of the quantum harmonic oscillator uses an explicitly non-relativistic expression for the kinetic energy of the oscillator, and is thus a quantum version of the classical harmonic oscillator.
Early attempts to merge quantum mechanics with special relativity involved the replacement of the Schrödinger equation with a covariant equation such as the Klein-Gordon equation or the Dirac equation. While these theories were successful in explaining many experimental results, they had certain unsatisfactory qualities stemming from their neglect of the relativistic creation and annihilation of particles. A fully relativistic quantum theory required the development of quantum field theory, which applies quantization to a field rather than a fixed set of particles. The first complete quantum field theory, quantum electrodynamics, provides a fully quantum description of the electromagnetic interaction.
The full apparatus of quantum field theory is often unnecessary for describing electrodynamic systems. A simpler approach, one employed since the inception of quantum mechanics, is to treat charged particles as quantum mechanical objects being acted on by a classical electromagnetic field. For example, the elementary quantum model of the hydrogen atom describes the electric field of the hydrogen atom using a classical Coulomb potential. This "semi-classical" approach fails if quantum fluctuations in the electromagnetic field play an important role, such as in the emission of photons by charged particles.
Quantum field theories for the strong nuclear force and the weak nuclear force have been developed. The quantum field theory of the strong nuclear force is called quantum chromodynamics, and describes the interactions of the subnuclear particles: quarks and gluons. The weak nuclear force and the electromagnetic force were unified, in their quantized forms, into a single quantum field theory known as electroweak theory, by the physicists Carl Jamieson, Sheldon Glashow and Steven Weinberg.
It has proven difficult to construct quantum models of gravity, the remaining fundamental force. Semi-classical approximations are workable, and have led to predictions such as Hawking radiation. However, the formulation of a complete theory of quantum gravity is hindered by apparent incompatibilities between general relativity, the most accurate theory of gravity currently known, and some of the fundamental assumptions of quantum theory. The resolution of these incompatibilities is an area of active research, and theories such as string theory are among the possible candidates for a future theory of quantum gravity.
In the 21st century classical mechanics has been extended into the complex domain and complex classical mechanics exhibits behaviours very similar to quantum mechanics.
|
|
The particle in a 1-dimensional potential energy box is the most simple example where restraints lead to the quantization of energy levels. The box is defined as zero potential energy inside a certain interval and infinite everywhere outside that interval. For the 1-dimensional case in the x direction, the time-independent Schrödinger equation can be written as:
Attempts at a unified field theory
As of 2010 the quest for unifying the fundamental forces through quantum mechanics is still ongoing. Quantum electrodynamics (or "quantum electromagnetism"), which is currently the most accurately tested physical theory,[35] has been successfully merged with the weak nuclear force into the electroweak force and work is currently being done to merge the electroweak and strong force into the electrostrong force. Current predictions state that at around 1014 GeV the three aforementioned forces are fused into a single unified field,[36] Beyond this "grand unification", it is speculated that it may be possible to merge gravity with the other three gauge symmetries, expected to occur at roughly 1019 GeV. However - and while special relativity is parsimoniously incorporated into quantum electrodynamics - the expanded general relativity, currently the best theory describing the gravitation force, has not been fully incorporated into quantum theory. |
Relativity and quantum mechanics  |
Even with the defining postulates of both Einstein's theory of general relativity and quantum theory being indisputably supported by rigorous and repeated empirical evidence and while they do not directly contradict each other theoretically (at least with regard to primary claims), they are resistant to being incorporated within one cohesive model.
Einstein himself is well known for rejecting some of the claims of quantum mechanics. While clearly contributing to the field, he did not accept the more philosophical consequences and interpretations of quantum mechanics, such as the lack of deterministic causality and the assertion that a single subatomic particle can occupy numerous areas of space at one time. He also was the first to notice some of the apparently exotic consequences of entanglement and used them to formulate the Einstein-Podolsky-Rosen paradox, in the hope of showing that quantum mechanics had unacceptable implications. This was 1935, but in 1964 it was shown by John Bell (see Bell inequality) that Einstein's assumption was correct, but had to be completed by hidden variables and thus based on wrong philosophical assumptions. According to the paper of J. Bell and the Copenhagen interpretation (the common interpretation of quantum mechanics by physicists since 1927), and contrary to Einstein's ideas, quantum mechanics was
- neither a "realistic" theory (since quantum measurements do not state pre-existing properties, but rather they prepare properties)
The Einstein-Podolsky-Rosen paradox shows in any case that there exist experiments by which one can measure the state of one particle and instantaneously change the state of its entangled partner, although the two particles can be an arbitrary distance apart; however, this effect does not violate causality, since no transfer of information happens. These experiments are the basis of some of the most topical applications of the theory, quantum cryptography, which has been on the market since 2004 and works well, although at small distances of typically 1000 km.
Gravity is negligible in many areas of particle physics, so that unification between general relativity and quantum mechanics is not an urgent issue in those applications. However, the lack of a correct theory of quantum gravity is an important issue in cosmology and physicists' search for an elegant "theory of everything". Thus, resolving the inconsistencies between both theories has been a major goal of twentieth- and twenty-first-century physics. Many prominent physicists, including Stephen Hawking, have labored in the attempt to discover a theory underlying everything, combining not only different models of subatomic physics, but also deriving the universe's four forces —the strong force, electromagnetism, weak force, and gravity— from a single force or phenomenon. One of the leaders in this field is Edward Witten, a theoretical physicist who formulated the groundbreaking M-theory, which is an attempt at describing the supersymmetrical based string theory. |
Applications  |
Quantum mechanics has had enormous success in explaining many of the features of our world. The individual behaviour of the subatomic particles that make up all forms of matter—electrons, protons, neutrons, photons and others—can often only be satisfactorily described using quantum mechanics. Quantum mechanics has strongly influenced string theory, a candidate for a theory of everything (see reductionism) and the multiverse hypothesis. It is also related to statistical mechanics.
Quantum mechanics is important for understanding how individual atoms combine covalently to form chemicals or molecules. The application of quantum mechanics to chemistry is known as quantum chemistry. (Relativistic) quantum mechanics can in principle mathematically describe most of chemistry. Quantum mechanics can provide quantitative insight into ionic and covalent bonding processes by explicitly showing which molecules are energetically favorable to which others, and by approximately how much. Most of the calculations performed in computational chemistry rely on quantum mechanics.
Much of modern technology operates at a scale where quantum effects are significant. Examples include the laser, the transistor (and thus the microchip), the electron microscope, and magnetic resonance imaging. The study of semiconductors led to the invention of the diode and the transistor, which are indispensable for modern electronics.
Researchers are currently seeking robust methods of directly manipulating quantum states. Efforts are being made to develop quantum cryptography, which will allow guaranteed secure transmission of information. A more distant goal is the development of quantum computers, which are expected to perform certain computational tasks exponentially faster than classical computers. Another active research topic is quantum teleportation, which deals with techniques to transmit quantum states over arbitrary distances.
Quantum tunneling is vital in many devices, even in the simple light switch, as otherwise the electrons in the electric current could not penetrate the potential barrier made up of a layer of oxide. Flash memory chips found in USB drives use quantum tunneling to erase their memory cells.
QM primarily applies to the atomic regimes of matter and energy, but some systems exhibit quantum mechanical effects on a large scale; superfluidity (the frictionless flow of a liquid at temperatures near absolute zero) is one well-known example. Quantum theory also provides accurate descriptions for many previously unexplained phenomena such as black body radiation and the stability of electron orbitals. It has also given insight into the workings of many different biological systems, including smell receptors and protein structures.[40] Even so, classical physics often can be a good approximation to results otherwise obtained by quantum physics, typically in circumstances with large numbers of particles or large quantum numbers. (However, some open questions remain in the field of quantum chaos.) |
Philosophical Consequences  |
The Copenhagen interpretation, due largely to the Danish theoretical physicist Niels Bohr, is the interpretation of quantum mechanics most widely accepted amongst physicists. According to it, the probabilistic nature of quantum mechanics predictions cannot be explained in terms of some other deterministic theory, and does not simply reflect our limited knowledge. Quantum mechanics provides probabilistic results because the physical universe is itself probabilistic rather than deterministic.
Albert Einstein, himself one of the founders of quantum theory, disliked this loss of determinism in measurement (this dislike is the source of his famous quote, "God does not play dice with the universe."). Einstein held that there should be a local hidden variable theory underlying quantum mechanics and that, consequently, the present theory was incomplete. He produced a series of objections to the theory, the most famous of which has become known as the Einstein-Podolsky-Rosen paradox. John Bell showed that the EPR paradox led to experimentally testable differences between quantum mechanics and local realistic theories. Experiments have been performed confirming the accuracy of quantum mechanics, thus demonstrating that the physical world cannot be described by local realistic theories.[41] The Bohr-Einstein debates provide a vibrant critique of the Copenhagen Interpretation from an epistemological point of view.
The Everett many-worlds interpretation, formulated in 1956, holds that all the possibilities described by quantum theory simultaneously occur in a multiverse composed of mostly independent parallel universes.[42] This is not accomplished by introducing some new axiom to quantum mechanics, but on the contrary by removing the axiom of the collapse of the wave packet: All the possible consistent states of the measured system and the measuring apparatus (including the observer) are present in a real physical (not just formally mathematical, as in other interpretations) quantum superposition. Such a superposition of consistent state combinations of different systems is called an entangled state.
While the multiverse is deterministic, we perceive non-deterministic behavior governed by probabilities, because we can observe only the universe, i.e. the consistent state contribution to the mentioned superposition, we inhabit. Everett's interpretation is perfectly consistent with John Bell's experiments and makes them intuitively understandable. However, according to the theory of quantum decoherence, the parallel universes will never be accessible to us. This inaccessibility can be understood as follows: Once a measurement is done, the measured system becomes entangled with both the physicist who measured it and a huge number of other particles, some of which are photons flying away towards the other end of the universe; in order to prove that the wave function did not collapse one would have to bring all these particles back and measure them again, together with the system that was measured originally. This is completely impractical, but even if one could theoretically do this, it would destroy any evidence that the original measurement took place (including the physicist's memory).
|
|


Double slit experiment

Hexagon with hexagram inside
Tetrahedron with the sheres


OM

Octave

Sextagon with six pointed light

Torus in the sphere





Full pet

Flower of life in the sphere

Edge star

3D star tetrahedron

512

Filled sphere

Hollow sphere

Nosphere

Low pressure system over iceland
Swastika |
|
2 Art 
Circles, Triangles and squares

Bar magnet gravity bar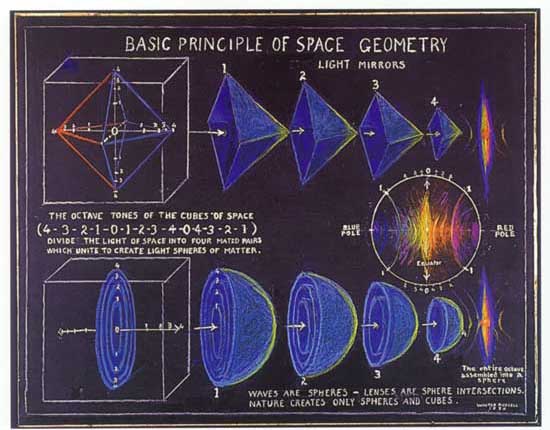
Basic Principle of Space Geometry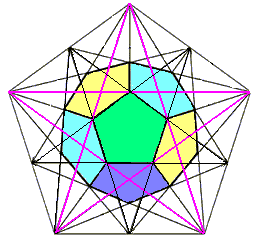
Pentogram pentogon illustration
Four Leaf Clover

Vesica Piscis

Interdimensional Space

Dharma Wheel

Spiral illustration

September Fantasy
Cross section

Flower of life

The geometry code

Spiral illustration

Spiral art
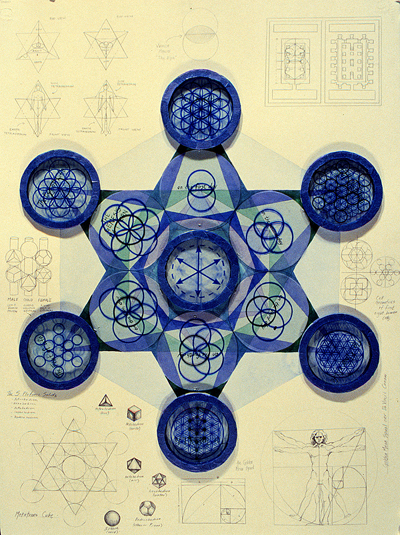
Sextagon art

Jade Temple Yantra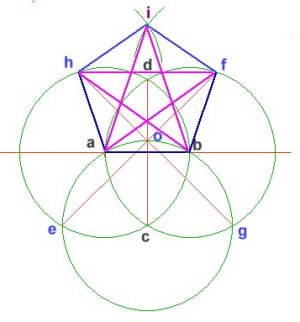
Pentogram and circles
Living vortex

Pentogram glass

Hexagon with hexagram inside
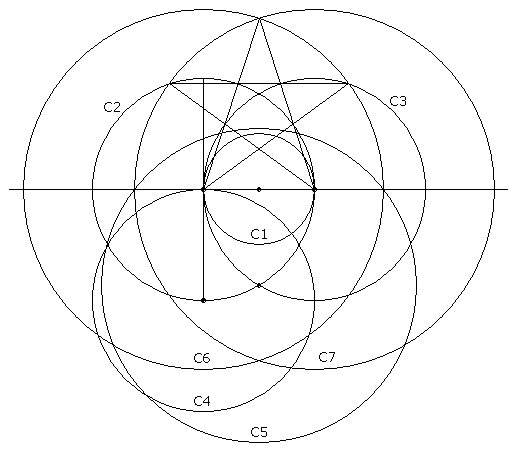
Penta construction

Star fractal

Digital art fractal

Golden mean spiral
The flower of life

Flower of life and tree of life
Polyhedron sculpture
Sextagon

OM

Interesting shape
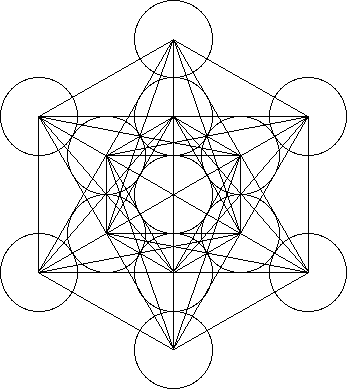
Metatrons cube

Midsummer nights dream art
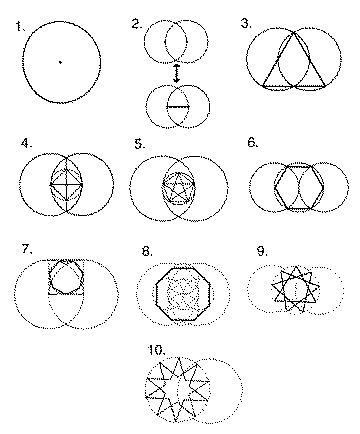
Geometric figures

Star tetrahydron sculpture

The flower of life

Flower of life illustration
Septogram and Septogon
Art

Overlapping circles
Overlapping circles 
OM |
Mandala  |
In various spiritual traditions, mandalas may be employed for focusing attention of aspirants and adepts, as a spiritual teaching tool, for establishing a sacred space, and as an aid to meditation and trance induction. According to David Fontana, its symbolic nature can help one "to access progressively deeper levels of the unconscious, ultimately assisting the meditator to experience a mystical sense of oneness with the ultimate unity from which the cosmos in all its manifold forms arises." [3] The psychoanalyst Carl Jung saw the mandala as "a representation of the unconscious self,"[citation needed] and believed his paintings of mandalas enabled him to identify emotional disorders and work towards wholeness in personality.[4]
In common use, mandala has become a generic term for any plan, chart or geometric pattern that represents the cosmos metaphysically or symbolically, a microcosm of the Universe from the human perspective.
Hinduism 
The term yantra normally refers to Hindu contexts and practices, while mandala normally refers to Buddhist contexts and practices. Yet, the terms are also used interchangeably, and mandala is sometimes used as a cross-over term in Hindu contexts.
A yantra is a two- or three-dimensional geometric composition used in sadhanas, or meditative rituals. It is thought to be the abode of the deity. Each yantra is unique and calls the deity into the presence of the practitioner through the elaborate symbolic geometric designs. According to one scholar, “Yantras function as revelatory symbols of cosmic truths and as instructional charts of the spiritual aspect of human experience"
Many situate yantras as central focus points for Hindu tantric practice.Yantras are not representations, but are lived, experiential, nondual realities. As Khanna describes:
Despite its cosmic meanings a yantra is a reality lived. Because of the relationship that exists in the Tantras between the outer world (the macrocosm) and man’s [sic] inner world (the microcosm), every symbol in a yantra is ambivalently resonant in inner-outer synthesis, and is associated with the subtle body and aspects of human consciousness.[6]
Mandala is also the term used to describe the Rig Veda, a sacred Hindu scripture.
Buddhism 
Early and Theravada Buddhism 
The mandala can be found in the form of the Stupa and in the Atanatiya Sutta in the Digha Nikaya, part of the Pali Canon. This text is frequently chanted.
Tibetan Vajrayana 
A kyil khor (དཀྱིལ་འཁོར།; Tibetan for mandala) in Vajrayana Buddhism usually depicts a landscape of the "Buddha-land," or the enlightened vision of a Buddha, which inevitably represents the nature of experience and the intricacies of both the enlightened and confused mind, or "a microcosm representing various divine powers at work in the universe." Such mandalas consist of an outer circular mandala and an inner square (or sometimes circular) mandala with an ornately decorated mandala "palace" placed at the center. Any part of the inner mandala can be occupied by Buddhist glyphs and symbols, as well as by images of its associated deities, which "symbolise different stages in the process of the realisation of the truth."
Mandalas are commonly used by tantric Buddhists as an aid to meditation. More specifically, a Buddhist mandala is envisaged as a "sacred space," a "Pure Buddha Realm," and also as an abode of fully realised beings or deities. While on the one hand, the mandala is regarded as a place separated and protected from the ever-changing and impure outer world of samsara, and is thus seen as a "Buddhafield" or a place of Nirvana and peace, the view of Vajrayana Buddhism sees the greatest protection from samsara being the power to see samsaric confusion as the "shadow" of purity (which then points towards it). By visualizing "pure lands," one learns to understand experience itself as pure, and as the abode of enlightenment. The protection that we need, in this view, is from our own minds, as much as from external sources of confusion. In many tantric mandalas, this aspect of separation and protection from the outer samsaric world is depicted by "the four outer circles: the purifying fire of wisdom, the vajra circle, the circle with the eight tombs, the lotus circle." The ring of vajras forms a connected fence-like arrangement running around the perimeter of the outer mandala circle.
The mandala is also "a support for the meditating person," something to be repeatedly contemplated to the point of saturation, such that the image of the mandala becomes fully internalised in even the minutest detail and can then be summoned and contemplated at will as a clear and vivid visualised image. With every mandala comes what Tucci calls "its associated liturgy...contained in texts known as tantras," instructing practitioners on how the mandala should be drawn, built and visualised, and indicating the mantras to be recited during its ritual use.
As a meditation on impermanence (a central teaching of Buddhism), after days or weeks of creating the intricate pattern of a sand mandala, the sand is brushed together and placed in a body of running water to spread the blessings of the mandala.
A mandala can also represent the entire universe, which is traditionally depicted with Mount Meru as the axis mundi in the center, surrounded by the continents.[18] A "mandala offering"[19] in Tibetan Buddhism is a symbolic offering of the entire universe. Every intricate detail of these mandalas is fixed in the tradition and has specific symbolic meanings, often on more than one level.
The mandala can be shown to represent in visual form the core essence of the Vajrayana teachings. In the mandala, the outer circle of fire usually symbolises wisdom. The ring of 8 charnel grounds[20] represents the Buddhist exhortation to always be mindful of death, and the impermanence with which samsara is suffused: "such locations were utilized in order to confront and to realize the transient nature of life."[21] Described elsewhere: "within a flaming rainbow nimbus and encircled by a black ring of dorjes, the major outer ring depicts the eight great charnel grounds, to emphasize the dangerous nature of human life."[22] Inside these rings lie the walls of the mandala palace itself, specifically a place populated by deities and Buddhas.
One well-known type of mandala, in Japan is the mandala of the "Five Buddhas", archetypal Buddha forms embodying various aspects of enlightenment. Such Buddhas are depicted depending on the school of Buddhism, and even the specific purpose of the mandala. A common mandala of this type is that of the Five Wisdom Buddhas (a.k.a. Five Jinas), the Buddhas Vairocana, Aksobhya, Ratnasambhava, Amitabha and Amoghasiddhi. When paired with another mandala depicting the Five Wisdom Kings, this forms the Mandala of the Two Realms.
Offerings
Whereas the above mandala represents the pure surroundings of a Buddha, this mandala represents the universe. This type of mandala is used for the mandala-offerings, during which one symbolically offers the universe to the Buddhas or to one's teacher. Within Vajrayana practice, 100,000 of these mandala offerings (to create merit) can be part of the preliminary practices before a student even begins actual tantric practices.[23] This mandala is generally structured according to the model of the universe as taught in a Buddhist classic text the Abhidharma-kośa, with Mount Meru at the centre, surrounded by the continents, oceans and mountains, etc.
Shingon Buddhism 
The Japanese branch of Vajrayana Buddhism -- Shingon Buddhism—makes frequent use of mandalas in its rituals as well, though the actual mandalas differ. When Shingon's founder, Kukai, returned from his training in China, he brought back two mandalas that became central to Shingon ritual: the Mandala of the Womb Realm and the Mandala of the Diamond Realm.
These two mandalas are engaged in the abhiseka initiation rituals for new Shingon students, more commonly known as the Kechien Kanjō (結縁灌頂). A common feature of this ritual is to blindfold the new initiate and to have them throw a flower upon either mandala. Where the flower lands assists in the determination of which tutelary deity the initiate should follow.
Sand Mandalas, as found in Tibetan Buddhism, are not practiced in Shingon Buddhism.
Nichiren Buddhism
The mandala in Nichiren Buddhism is called a moji-mandala (文字曼陀羅) and is a hanging paper scroll or wooden tablet whose inscription consists of Chinese characters and medieval-Sanskrit script representing elements of the Buddha's enlightenment, protective Buddhist deities, and certain Buddhist concepts. Called the Gohonzon, it was originally inscribed by Nichiren, the founder of this branch of Japanese Buddhism, during the late 13th Century. The Gohonzon is the primary object of veneration in some Nichiren schools and the only one in others, which consider it to be the supreme object of worship as the embodiment of the supreme Dharma and Nichiren's inner enlightenment. The seven characters Nam Myoho Renge Kyo, considered to be the name of the supreme Dharma, as well as the invocation that believers chant, are written down the center of all Nichiren-sect Gohonzons, whose appearance may otherwise vary depending on the particular school and other factors.
Pure Land Buddhism
Mandalas have sometimes been used in Pure Land Buddhism to graphically represent the Pure Land, based on descriptions found in the Larger Sutra and the Contemplation Sutra. The most famous mandala in Japan is the Taima Mandala, dated to approximately 763 CE. The Taima Mandala is based upon the Contemplation Sutra, but other similar mandalas have been made subsequently. Unlike mandalas used in Vajrayana Buddhism, it is not used as an object of meditation or for esoteric ritual. Instead, it provides a visual pictorial of the Pure Land texts, and is used as a teaching aid.[citation needed]
Also in Jodo Shinshu Buddhism, Shinran and his descendant, Rennyo, sought a way to create easily accessible objects of reverence for the lower-classes of Japanese society. Shinran designed a mandala using a hanging scroll, and the words of the nembutsu (南無阿彌陀佛) written vertically. This style of mandala is still used by some Jodo Shinshu Buddhists in home altars, or butsudan.
Christianity
Cowen (2005), states that forms which are evocative of mandalas are prevalent in Christianity: the celtic cross; the rosary; the halo; the aureole; oculi; the Crown of Thorns; rose windows; the Rosy Cross; and the dromenon on the floor of Chartres Cathedral. The dromenon represents a journey from the outer world to the inner sacred centre where the Divine is found.[24]
Similarly, many of the Illuminations of Hildegard von Bingen can be used as mandalas, as well as many of the images of esoteric Christianity, as in Christian Hermeticism, Christian Alchemy, and Rosicrucianism.
Bora ring
A Bora is the name given both to an initiation ceremony of Indigenous Australians, and to the site Bora Ring on which the initiation is performed. At such a site, young boys are transformed into men via rites of passage. The word Bora was originally from South-East Australia, but is now often used throughout Australia to describe an initiation site or ceremony. The term "bora" is held to be etymologically derived from that of the belt or girdle that encircles initiated men. The appearance of a Bora Ring varies from one culture to another, but it is often associated with stone arrangements, rock engravings, or other art works. Women are generally prohibited from entering a bora. In South East Australia, the Bora is often associated with the creator-spirit Baiame.
Bora rings, found in South-East Australia, are circles of foot-hardened earth surrounded by raised embankments. They were generally constructed in pairs (although some sites have three), with a bigger circle about 22 metres in diameter and a smaller one of about 14 metres. The rings are joined by a sacred walkway. Matthews (1897)[25] gives an eye-witness account of a Bora ceremony, and explains the use of the two circles.
|
|

Sextogram art

Pentagon exponentially growing

Tibetan sand mandala
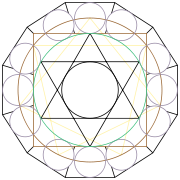
Sextagon in a dodecagon

Sri Yantra Construct

Flower fractal

Tibetan mandala goddess

air atlantean basshub
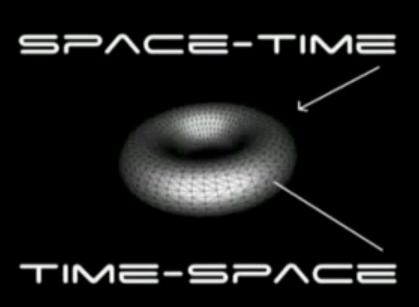
Time space vs space time

Time space vs space time
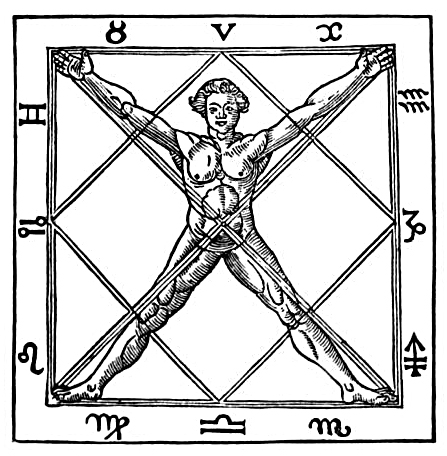
Human and the square

Tibetans making Mandalas

Tibetan Mandala

Pentagona and the head

Flower of life and flowers

Square flactal

3D sacred geometry toys

Star flower

Blue star

Five pointed star in a circle

Tibetan infinity

Circles, squares and triangles

The laticework of the universe

Flower of life

DNA Web

Swastika
 Metatrons Cube
Metatrons Cube
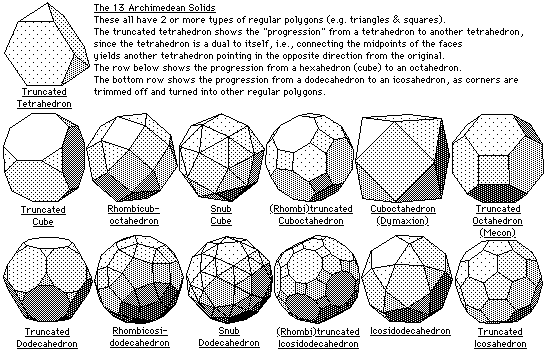
Vibration mutation

Solar taurus
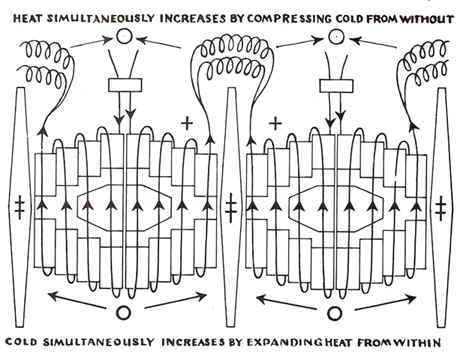
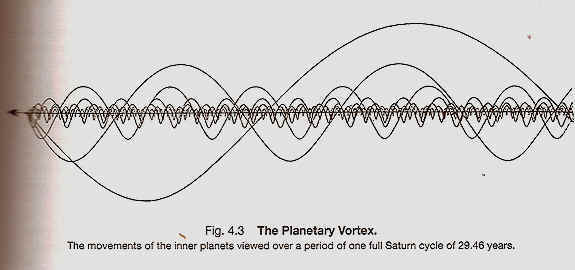
The Rotary Vortex
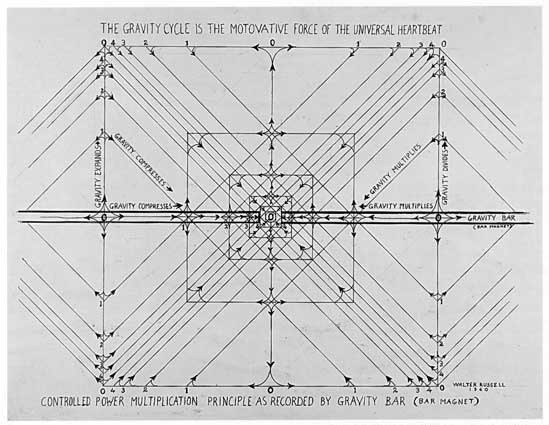
The gravity cycle
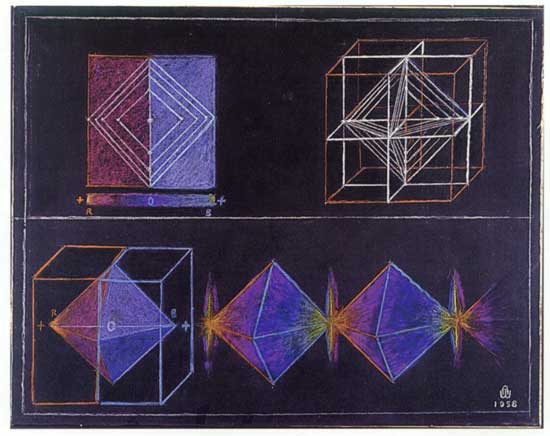
Tetrahedrons

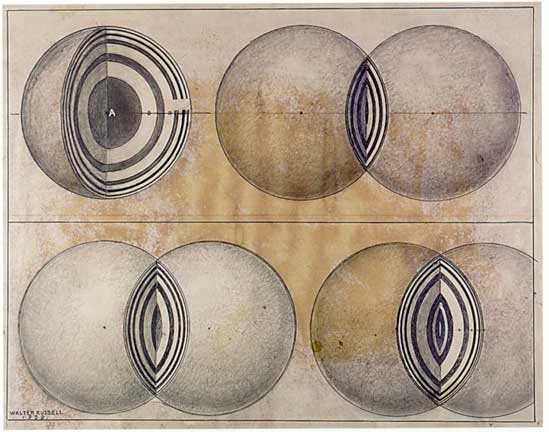
Overlapping circles


Atomic Tornados
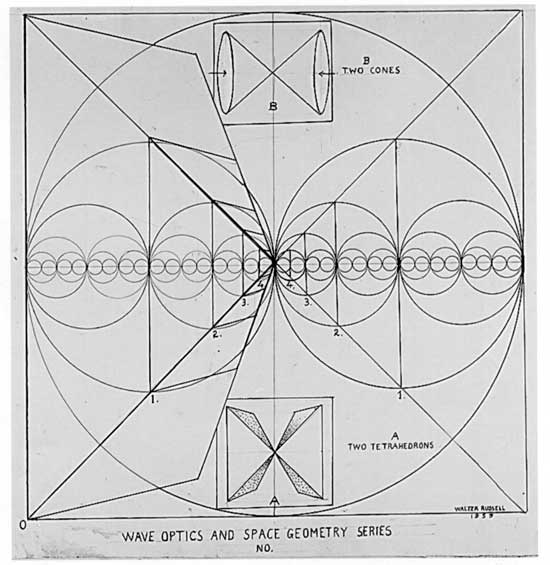
Wave optics and space geometry

Fractal portal art

Computer generated star fractal

Pentogram drawing

Sextogram and flower of life


Intricate flower of life

Sextogon inside Docegon

Septogram and Septogon

Tree of life point meanings
Petagram in a pentagon

Vortex art
map of the Universe

Tetrahedron in a sphere |
|
3 Geometry of the Body 
|
six feet of dna in one cell. wrap dna around the world 5 million times
|
|
|
Nature 
5 Sacred Geometry of Astronomical objects 
|
1 How waves travel 
|
Interconnecting Web of Life 
|
Vortexes 
|
|

Tornado vortex

Wave traveling into a vortex
cubic wave fiels and vortex cones |
|
Torus 
|
Male verses Female 
| |
|

Yin Yang |
|
4 Five Platonic Solids 
|
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and angles.
There are precisely five Platonic solids (shown below).
The name of each figure is derived from its number of faces: respectively 4, 6, 8, 12, and 20.[1]
The aesthetic beauty and symmetry of the Platonic solids have made them a favorite subject of geometers for thousands of years. They are named for the ancient Greek philosopher Plato who theorized that the classical elements were constructed from the regular solids.
|
History  |
|
The Platonic solids have been known since antiquity. Ornamented models of them can be found among the carved stone balls created by the late neolithic people of Scotland at least 1000 years before Plato (Atiyah and Sutcliffe 2003). Dice go back to the dawn of civilization with shapes that augured formal charting of Platonic solids.
The ancient Greeks studied the Platonic solids extensively. Some sources (such as Proclus) credit Pythagoras with their discovery. Other evidence suggests he may have only been familiar with the tetrahedron, cube, and dodecahedron, and that the discovery of the octahedron and icosahedron belong to Theaetetus, a contemporary of Plato. In any case, Theaetetus gave a mathematical description of all five and may have been responsible for the first known proof that there are no other convex regular polyhedra.
The Platonic solids feature prominently in the philosophy of Plato for whom they are named. Plato wrote about them in the dialogue Timaeus c.360 B.C. in which he associated each of the four classical elements (earth, air, water, and fire) with a regular solid. Earth was associated with the cube, air with the octahedron, water with the icosahedron, and fire with the tetrahedron. There was intuitive justification for these associations: the heat of fire feels sharp and stabbing (like little tetrahedra). Air is made of the octahedron; its minuscule components are so smooth that one can barely feel it. Water, the icosahedron, flows out of one's hand when picked up, as if it is made of tiny little balls. By contrast, a highly un-spherical solid, the hexahedron (cube) represents earth. These clumsy little solids cause dirt to crumble and break when picked up, in stark difference to the smooth flow of water. The fifth Platonic solid, the dodecahedron, Plato obscurely remarks, "...the god used for arranging the constellations on the whole heaven". Aristotle added a fifth element, aithêr (aether in Latin, "ether" in English) and postulated that the heavens were made of this element, but he had no interest in matching it with Plato's fifth solid.
Euclid gave a complete mathematical description of the Platonic solids in the Elements; the last book (Book XIII) of which is devoted to their properties. Propositions 13–17 in Book XIII describe the construction of the tetrahedron, octahedron, cube, icosahedron, and dodecahedron in that order. For each solid Euclid finds the ratio of the diameter of the circumscribed sphere to the edge length. In Proposition 18 he argues that there are no further convex regular polyhedra. Andreas Speiser has advocated the view that the construction of the 5 regular solids is the chief goal of the deductive system canonized in "Elements".[2] Much of the information in Book XIII is probably derived from the work of Theaetetus.
In the 16th century, the German astronomer Johannes Kepler attempted to find a relation between the five extraterrestrial planets known at that time and the five Platonic solids. In Mysterium Cosmographicum, published in 1596, Kepler laid out a model of the solar system in which the five solids were set inside one another and separated by a series of inscribed and circumscribed spheres. The six spheres each corresponded to one of the planets (Mercury, Venus, Earth, Mars, Jupiter, and Saturn). The solids were ordered with the innermost being the octahedron, followed by the icosahedron, dodecahedron, tetrahedron, and finally the cube. In this way the structure of the solar system and the distance relationships between the planets was dictated by the Platonic solids. In the end, Kepler's original idea had to be abandoned, but out of his research came the recognition that the orbits of planets are ellipses rather than circles, as well as his two laws of orbital dynamics, changing the courses of physics and astronomy, plus the discovery of the Kepler solids. |
Combinatorial properties  |
A convex polyhedron is a Platonic solid if and only if
Each Platonic solid can therefore be denoted by a symbol {p, q} where
- p = the number of edges of each face (or the number of vertices of each face) and
- q = the number of faces meeting at each vertex (or the number of edges meeting at each vertex).
The symbol { p, q}, called the Schläfli symbol, gives a combinatorial description of the polyhedron. The Schläfli symbols of the five Platonic solids are given in the table below.
All other combinatorial information about these solids, such as total number of vertices (V), edges (E), and faces (F), can be determined from p and q. Since any edge joins two vertices and has two adjacent faces we must have:
The other relationship between these values is given by Euler's formula:
This nontrivial fact can be proved in a great variety of ways (in algebraic topology it follows from the fact that the Euler characteristic of the sphere is 2). Together these three relationships completely determine V, E, and F:
Note that swapping p and q interchanges F and V while leaving E unchanged (For a geometric interpretation of this fact see the section on dual polyhedra below). |
Classification  |
| It is a classical result that there are only five convex regular polyhedra. Two common arguments are given below. Both of these arguments only show that there can be no more than five Platonic solids. That all five actually exist is a separate question—one that can be answered by an explicit construction. |
Geometric proof  |
The following geometric argument is very similar to the one given by Euclid in the Elements:
- Each vertex of the solid must coincide with one vertex each of at least three faces.
- At each vertex of the solid, the total, among the adjacent faces, of the angles between their respective adjacent sides must be less than 360°.
- The angles at all vertices of all faces of a Platonic solid are identical, so each vertex of each face must contribute less than 360°/3=120°.
- Regular polygons of six or more sides have only angles of 120° or more, so the common face must be the triangle, square, or pentagon. And for:
- Triangular faces: each vertex of a regular triangle is 60°, so a shape may have 3, 4, or 5 triangles meeting at a vertex; these are the tetrahedron, octahedron, and icosahedron respectively.
- Square faces: each vertex of a square is 90°, so there is only one arrangement possible with three faces at a vertex, the cube.
- Pentagonal faces: each vertex is 108°; again, only one arrangement, of three faces at a vertex is possible, the dodecahedron.
|
Topological proof  |
A purely topological proof can be made using only combinatorial information about the solids. The key is Euler's observation that V − E + F = 2, and the fact that pF = 2 E = qV. Combining these equations one obtains the equation Simple algebraic manipulation then gives
Since E is strictly positive we must have
Using the fact that p and q must both be at least 3, one can easily see that there are only five possibilities for {p, q}: |
Geometric properties  |
Angles  |
| There are a number of angles associated with each Platonic solid. The dihedral angle is the interior angle between any two face planes. The dihedral angle, θ, of the solid {p,q} is given by the formula
This is sometimes more conveniently expressed in terms of the tangent by
The quantity h is 4, 6, 6, 10, and 10 for the tetrahedron, cube, octahedron, dodecahedron, and icosahedron respectively.
The angular deficiency at the vertex of a polyhedron is the difference between the sum of the face-angles at that vertex and 2π. The defect, δ, at any vertex of the Platonic solids {p,q} is
By a theorem of Descartes, this is equal to 4π divided by the number of vertices (i.e. the total defect at all vertices is 4π).
The 3-dimensional analog of a plane angle is a solid angle. The solid angle, Ω, at the vertex of a Platonic solid is given in terms of the dihedral angle by
This follows from the spherical excess formula for a spherical polygon and the fact that the vertex figure of the polyhedron {p,q} is a regular q-gon.
The solid angle of a face subtended from the center of a platonic solid is equal to the solid angle of a full sphere (4π steradians) divided by the number of faces. Note that this is equal to the angular deficiency of its dual.
The various angles associated with the Platonic solids are tabulated below. The numerical values of the solid angles are given in steradians. The constant φ = (1+√5)/2 is the golden ratio. |
Radii, area, and volume  |
Another virtue of regularity is that the Platonic solids all possess three concentric spheres:
The radii of these spheres are called the circumradius, the midradius, and the inradius. These are the distances from the center of the polyhedron to the vertices, edge midpoints, and face centers respectively. The circumradius R and the inradius r of the solid {p, q} with edge length a are given by
where θ is the dihedral angle. The midradius ρ is given by
where h is the quantity used above in the definition of the dihedral angle (h = 4, 6, 6, 10, or 10). Note that the ratio of the circumradius to the inradius is symmetric in p and q:
The surface area, A, of a Platonic solid { p, q} is easily computed as area of a regular p-gon times the number of faces F. This is: The volume is computed as F times the volume of the pyramid whose base is a regular p-gon and whose height is the inradius r. That is,
The following table lists the various radii of the Platonic solids together with their surface area and volume. The overall size is fixed by taking the edge length, a, to be equal to 2.
The constants φ and ξ in the above are given by
Among the Platonic solids, either the dodecahedron or the icosahedron may be seen as the best approximation to the sphere. The icosahedron has the largest number of faces, the largest dihedral angle, and it hugs its inscribed sphere the tightest. The dodecahedron, on the other hand, has the smallest angular defect, the largest vertex solid angle, and it fills out its circumscribed sphere the most. |
Symmetry  |
Dual polyhedra  |
Every polyhedron has a dual polyhedron with faces and vertices interchanged. The dual of every Platonic solid is another Platonic solid, so that we can arrange the five solids into dual pairs.
- The tetrahedron is self-dual (i.e. its dual is another tetrahedron).
- The cube and the octahedron form a dual pair.
- The dodecahedron and the icosahedron form a dual pair.
If a polyhedron has Schläfli symbol { p, q}, then its dual has the symbol { q, p}. Indeed every combinatorial property of one Platonic solid can be interpreted as another combinatorial property of the dual.
One can construct the dual polyhedron by taking the vertices of the dual to be the centers of the faces of the original figure. The edges of the dual are formed by connecting the centers of adjacent faces in the original. In this way, the number of faces and vertices is interchanged, while the number of edges stays the same.
More generally, one can dualize a Platonic solid with respect to a sphere of radius d concentric with the solid. The radii (R, ρ, r) of a solid and those of its dual (R*, ρ*, r*) are related by
It is often convenient to dualize with respect to the midsphere (d = ρ) since it has the same relationship to both polyhedra. Taking d2 = Rr gives a dual solid with the same circumradius and inradius (i.e. R* = R and r* = r). |
Symmetry groups  |
In mathematics, the concept of symmetry is studied with the notion of a mathematical group. Every polyhedron has an associated symmetry group, which is the set of all transformations (Euclidean isometries) which leave the polyhedron invariant. The order of the symmetry group is the number of symmetries of the polyhedron. One often distinguishes between the full symmetry group, which includes reflections, and the proper symmetry group, which includes only rotations.
The symmetry groups of the Platonic solids are known as polyhedral groups (which are a special class of the point groups in three dimensions). The high degree of symmetry of the Platonic solids can be interpreted in a number of ways. Most importantly, the vertices of each solid are all equivalent under the action of the symmetry group, as are the edges and faces. One says the action of the symmetry group is transitive on the vertices, edges, and faces. In fact, this is another way of defining regularity of a polyhedron: a polyhedron is regular if and only if it is vertex-uniform, edge-uniform, and face-uniform.
There are only three symmetry groups associated with the Platonic solids rather than five, since the symmetry group of any polyhedron coincides with that of its dual. This is easily seen by examining the construction of the dual polyhedron. Any symmetry of the original must be a symmetry of the dual and vice-versa. The three polyhedral groups are:
The orders of the proper (rotation) groups are 12, 24, and 60 respectively — precisely twice the number of edges in the respective polyhedra. The orders of the full symmetry groups are twice as much again (24, 48, and 120). See (Coxeter 1973) for a derivation of these facts.
The following table lists the various symmetry properties of the Platonic solids. The symmetry groups listed are the full groups with the rotation subgroups given in parenthesis (likewise for the number of symmetries). Wythoff's kaleidoscope construction is a method for constructing polyhedra directly from their symmetry groups. We list for reference Wythoff's symbol for each of the Platonic solids.
|
In nature and technology  |
The tetrahedron, cube, and octahedron all occur naturally in crystal structures. These by no means exhaust the numbers of possible forms of crystals. However, neither the regular icosahedron nor the regular dodecahedron are amongst them. One of the forms, called the pyritohedron (named for the group of minerals of which it is typical) has twelve pentagonal faces, arranged in the same pattern as the faces of the regular dodecahedron. The faces of the pyritohedron are, however, not regular, so the pyritohedron is also not regular.
Circogonia icosahedra, a species of Radiolaria, shaped like a regular icosahedron.
In the early 20th century, Ernst Haeckel described (Haeckel, 1904) a number of species of Radiolaria, some of whose skeletons are shaped like various regular polyhedra. Examples include Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus and Circorrhegma dodecahedra. The shapes of these creatures should be obvious from their names.
Many viruses, such as the herpes virus, have the shape of a regular icosahedron. Viral structures are built of repeated identical protein subunits and the icosahedron is the easiest shape to assemble using these subunits. A regular polyhedron is used because it can be built from a single basic unit protein used over and over again; this saves space in the viral genome.
In meteorology and climatology, global numerical models of atmospheric flow are of increasing interest which employ grids that are based on an icosahedron (refined by triangulation) instead of the more commonly used longitude/latitude grid. This has the advantage of evenly distributed spatial resolution without singularities (i.e. the poles) at the expense of somewhat greater numerical difficulty.
Geometry of space frames is often based on platonic solids. In MERO system, Platonic solids are used for naming convention of various space frame configurations. For example ½O+T refers to a configuration made of one half of octahedron and a tetrahedron.
Several Platonic hydrocarbons have been synthesised, including cubane and dodecahedrane.
Platonic solids are often used to make dice, because dice of these shapes can be made fair. 6-sided dice are very common, but the other numbers are commonly used in role-playing games. Such dice are commonly referred to as dn where n is the number of faces (d8, d20, etc.); see dice notation for more details.
These shapes frequently show up in other games or puzzles. Puzzles similar to a Rubik's Cube come in all five shapes — see magic polyhedra. |
Related polyhedra and polytopes  |
Uniform polyhedra  |
| There exist four regular polyhedra which are not convex, called Kepler-Poinsot polyhedra. These all have icosahedral symmetry and may be obtained as stellations of the dodecahedron and the icosahedron.
The next most regular convex polyhedra after the Platonic solids are the cuboctahedron, which is a rectification of the cube and the octahedron, and the icosidodecahedron, which is a rectification of the dodecahedron and the icosahedron (the rectification of the self-dual tetrahedron is a regular octahedron). These are both quasi-regular meaning that they are vertex- and edge-uniform and have regular faces, but the faces are not all congruent (coming in two different classes). They form two of the thirteen Archimedean solids, which are the convex uniform polyhedra with polyhedral symmetry.
The uniform polyhedra form a much broader class of polyhedra. These figures are vertex-uniform and have one or more types of regular or star polygons for faces. These include all the polyhedra mentioned above together with an infinite set of prisms, an infinite set of antiprisms, and 53 other non-convex forms.
The Johnson solids are convex polyhedra which have regular faces but are not uniform. |
Tessellations |
The three regular tessellations of the plane are closely related to the Platonic solids. Indeed, one can view the Platonic solids as the five regular tessellations of the sphere. This is done by projecting each solid onto a concentric sphere. The faces project onto regular spherical polygons which exactly cover the sphere. One can show that every regular tessellation of the sphere is characterized by a pair of integers {p, q} with 1/p + 1/q > 1/2. Likewise, a regular tessellation of the plane is characterized by the condition 1/p + 1/q = 1/2. There are three possibilities:
In a similar manner one can consider regular tessellations of the hyperbolic plane. These are characterized by the condition 1/ p + 1/ q < 1/2. There is an infinite family of such tessellations. |
Higher dimensions |
| In more than three dimensions, polyhedra generalize to polytopes, with higher-dimensional convex regular polytopes being the equivalents of the three-dimensional Platonic solids.
In the mid-19th century the Swiss mathematician Ludwig Schläfli discovered the four-dimensional analogues of the Platonic solids, called convex regular 4-polytopes. There are exactly six of these figures; five are analogous to the Platonic solids, while the sixth one, the 24-cell, has no lower-dimensional analogue.
In all dimensions higher than four, there are only three convex regular polytopes: the simplex, the hypercube, and the cross-polytope. In three dimensions, these coincide with the tetrahedron, the cube, and the octahedron. |
See also |
|
|
|
3 Computer generated fractals 
| |
|

Jay Jacobson fractal |
|
|
Numbers 
1 Particles and Feilds
1 Electron spin opposite to each other
|
| 2 Chemical properties relate to electrons orbits, how many there are in outermost
shell |
| 3 Electron like to close their shells, that is how molecules are made, covalent
bonding |
| 4 Moving electric charge creates magnetic
field |
| 5 Light a form of electromagnetic wave, so is radio |
| 6 Electromagnetic rays travel from electron to electron |
| 7 Photons have no mass |
8 3 kinds of quarks, 2 in P and N, up and down
P = 2 ups and 1 down 2/3+2/3 = 1
N = 2 downs and 1 up, 2/3-1/3 = 0 |
9 Exist only in triplets and pairs
paris called mesons - have mass |
10 Nucleons - components of nucleus
Quantum uncertainty- life span of quarks |
11 10,000,000,000,000,000,000,000
/sec,
22 OÕ's after one |
12 High energy turns them into particles as they appear and disappear, the more
energy the shorter existence
Gluons- Keep the quarks together
Weak force- Beta decay, neutrino, intermediate vector boson |
| 13 4 FORCES- 1) Gravity 2) Nuclear 3) strong 4) weak |
| 14 4 PARTICLES- 1) Up quark 2) Down quark 3) Electron 4) Neutrino |
| 15 New big electron formed in experiments |
| 16 Field quanta with no mass 1) Gravitons 2) Photons |
| 17 Gravity decreases inverse squarely |
| 18 Photons carry electromagnetism, much stronger than gravity, but cancels itself
out with + and - poles |
19 6 X 10(24) kg is mass of Earth
strong force 1, electromagnetism is 10(-2) (1% as strong), weak force 10(-13) (100
B as strong), |
20 loops of 'string' holding quarks together 10(-33) cm in diameter,
as much smaller than atom as atom is smaller
than solar system |
| 21 String vibration corresponds to photon and graviton vibration |
|
The ultra violet catastrophe
The reason we aren't burned to a
crisp is because the high frequency light
travels in particles of waves getting smaller as the frequency goes up and verses
longer waves. this light is
shot out when the electron shield breaks and light particles shoot out. The
difference in the radius of the
atom coincides with the energy states, the smaller, more energy.
|
|
Heisenbergs Uncertainty Principle
You can't measure the momentum and
position of an electron both at
once, only one at a time
|
|
Einstein
'Take care not to make intellect
our God, it has powerful muscles but no personality.'
me - 'Intellect is only spiritually appropriate if you use it to teach others,
if you intellectualize and don't
share, you should be meditating'.
|
|
|
2 Interesting Astronomical Numbers
1 10 Billion stars in
milky way, olympic swimming pool with drops of water
|
| 2 160K how high satellites are |
| 3 Moon 81 X smaller than earth, 15.5 CM AWAY |
4 Sun big beach ball 30 inches70 cm across and earth is 75 meters away the
size of a pea, mercury is 30M away the
size of a pinhead jupiter is 400 Meters away size of a tennis ball uranus 10
Aussie cent coin 1.5 Km away pluto
a speck 18 ks away.
Mercury - 58 M kilos 5000 K diameter solar system 4.6 B years old
Mars - Half Earths size
Saturn - 10X earths diameter
Neptune - 30X as far from sun as earth |
5 Meteors burn up 100K up at 100,000Kph
Super giants 100 - 200 X the suns diameter |
6 If the galaxy was as big as Australia stars would be almost invisible specs
200m apart and the solar system
is 20 MM across |
7 Nebula, hundreds of light years in size
Globular's- 10s of thousand to over a million stars, can be thousands per cubic
light year |
| 8 Galactic center 30K light years away |
| 9 Psychedelic guided imagery to conceptualize things |
| 10 Einstein 'The eternal mystery of
the world is its comprehensibility'. |
| 11 Avagadro's number- # of hydrogen atoms in one gram 6.022045 X 10(23) |
12 At 0 degrees Celsius one cubic centimeter of air has 4.5 X 10(19) molecules
of air and travels at 461 miles
per second or 17 K k/h, 3.5 B collisions/second
Newton's three laws- 1) object stays in motion 2) Force makes it accelerate 3)
Equal and opposite reaction
10(23)- stars in universe |
| 13 Cesium is biggest atom at .0000005 mm across, 10m to stretch across postage
stamps serrated edge |
| 14 Kelvin- atom is .1 nanometers across atom 10(-8) cm across, but nucleus 10(-13) |
15 Nucleus is 10(-15) of atom, one M of B
Isotope- Positive or negative charge atom, carbon
photon- light beam
92 - Protons in Uranium, 234 weight
10(12)- photons of light hit pinhead in a second |
16 Photons keep atom from collapsing
Planck's constant- Mass of photon 6.5 X 10(-27) |
| 17 Electron mass- 9 X 10(-28)G |
| 18 We are halfway between quanta and known universe |
19 Something 10(-27) cm across inside sugar cube is like sugar cubes spanning
1/10 of known universe one B light years
|
| 20 0 degrees Celsius oxygen molecule
moves 461 m/s, 17K KM/H |
| 21 Atom looses energy as electron moves closer to nucleus and gains it as it moves
away from nucleus |
| 22 Mass of electron is 9 X 10(-28) |
| 23 # stars in galaxy 10(11) |
| 24 So we are halfway between atom and universe |
| 25 Collapse of the wave function'? p 51 |
| 26 The more an electron is squeezed, the higher its velocity |
| 27 'Wave packet' keeps electron from hitting nucleus |
| 28 2 electrons in first level and 8 on each others |
|
|
3 Evolution 
1 Recessive genes- RR, RS, SR, SS 1/4
RR- rough seeds
|
| 2 1830's mendel's time, no belief in evolution |
3 After dinosaur death 65 million years ago, mammals had chance, rodents to dogs
in 3 million years, and 15 million
to elephants pig size |
| 4 98% our DNA same as Gorillas and chimps |
| 5 50% chance to share gene with with sibling and 1/8 change with first cousin |
| 6 Einstein-'The fact universe is comprehensible is a miracle' |
| 7 Everest is 8,85 km |
| 8 Air is 78% nitrogen |
8 150 years ago atmosphere had .028% carbon dioxide, now .035%
Venus 500 degrees C with 0 bars- atmospheric pressure at sea level |
| 9 Mars gets over freezing for a little every day |
| 10 Carbon dioxide molecule holds one photon, causing greenhouse effect |
| 11 Mars 1/10 mass of earth, too small to keep carbon dioxide |
12 Volcano's put carbon dioxide in the air
Photosenthisis- Chemical reactions caused by sunlight that produces carbon dioxide.
takes carbon dioxide out of
the air |
| 13 Oxygen - highly reactive substance, flame fast, rust slow |
| 14 1.5 B years single cell, then |
| 15 Atmosphere 1.6% of what it would be with out rain |
| 16 Ozone- 3 Oxygen molecules together caused by UV rays 15-50 km up recycled always |
| 17 Decades for ozone to cover from our damage |
| 18 Fossil shells bring carbon dioxide out of atmosphere |
| 19 Carbon dioxide released from high pressure in depths of earth |
| 20 Volcano's and rain keep equilibrium |
| 21 15 degrees C average temperature surface of earth |
| 22 Earth is wobbling gyroscope, 20,000 years to complete |
| 23 21.8-24.4 out of vertical, 41,000 years long cycle 23.4 today |
| 24 100,000 year long cycle of elliptical to circular orbit |
| 25 Because north pole is water, northern hemisphere is very sensitive to astronomical
influences |
26 Ice ages come when northern hemisphere gets cool enough to let snow stick and once
that happens there is a chain
reaction and takes longer to cool down with snow reflecting heart as little
as 200 years to go to ice age,
and many thousand to get out, Ice age 100,000 years long, and interglacial
10 to 20,000 years long |
| 27 Summers getting cooler now |
| 28 Drought caused by ice age caused us to bust out of jungle from over population |
| 29 Intelligent had advantage in challenging environment, causing evolution |
| 30 Our DNA is 99.8% similar to each other |
| 31 Apes evolved from man from droughts causing man to got o jungle- not |
| 32 Since industrial revolution, carbon dioxide in air went from .028-.035% |
| 33 World warmed 1 degree Celsius since 1880, one more degree in 20 ears, hotter
than more than 100,000 years |
|
|
4 Lives of Stars
| 1 10,000 years, recorded history less
than 100 human life times at 100 years |
| 2 Einstein- matter turns to energy |
| 3 Sun turn 5 M tons of matter to energy a second |
| 4 Alpha centauri, binary star, closest to 4.3 light years |
5 Milky way- Disk 13,000 light years thick
98,000 light years across, embedded in sphere of globular clusters 400,000
light years across |
| 6 Star must be 1/10 the mass of sun to glow, and with i 100 X suns mass to be
stable |
| 7 Nuclear fusion keeps star cool |
8 Gas clouds 1,000-10,000 molecules per cubic centimeter 755 hydrogen and 25%
Helium, form from being squeezed
from outside, then gravity brings them together |
9 Galactic sound wave from center caused by exploding stars squeezed matter together
as it passes like stirring
up cream in a drink, that is why it is a spiral galaxy. |
| 10 PARSEC- Arc second, 3.25 light years, 206,000 X earths distance to sun |
| 11 In this part of space, 1 star per 5 cubic parsecs of space, on Orion nebula,
stars are 1/10 parsec apart, 10,000 stars per parsec (3), after stars born they spread out in orbit around
milky way |
| 12 Nuclear fusion at 15 million degrees |
13 Star 25X mass of sun lives for 3 million years, sun lives 10,000 million years,
and one 1/2suns sue lives
200,000 million years, sun 1/2 through life |
14 After hydrogen is used up helium turns to carbon for B years in sun and is
a red giant as big as earths orbit
spewing out more complex elements and collapses so electrons snuggled up against
nucleus and turns to white dwarf
up against nucleus and turns to white dwarf 2/3 mass of the sun today the size
of the earth, 1 cm cubed weighs a
ton, million times density of water. today sun has million X volume of earth |
15 A dead star 1.4 X the mass of earth collapses again and electrons fuse with
proton and makes a neutron, reverse
beta decay and turns to neutron star 1.5X mass of sun is 10 kilometers across |
| 16 At formation of neutron star the by products are photons and neutrinos, CM(3)
weighs B tons |
17 A neutron star 3-4 x suns mass can't hold itself apart any more and
neutrons collapse into nothing and it turns
to a black hole, sucking even photons in |
| 18 Stars 11 solar masses, 11 X suns size, turn to black holes |
| 19 Neutron stars 10 billion degrees |
20 Super novas caused by the collapse of star into neutron star and bouncing
back a little and pushing incoming
material out and neutrinos also. ?To form planets later |
| 21 70 B neutrinos pass through a square cm of earth a second |
| 22 Gold is only made in supernova |
| 23 10 B neutrinos passed through our bodies in 87 from the supernova
160,000 light years away |
| 24 Solar system born from stuff of many supernovas, 1 atom in a thousand is heavier
than lithium |
|
|
5 Lives of Stars
1 10,000 years, recorded history less
than 100 human life times at 100 years
|
| 2 Einstein- matter turns to energy |
| 3 Sun turn 5 M tons of matter to energy a second |
| 4 Alpha centauri, binary star, closest to 4.3 light years |
| 5 Milky way- Disk 13,000 light years thick |
| 6 98,000 light years across, embedded in sphere of globular clusters 400,000
light years across |
| 7 Star must be 1/10 the mass of sun to glow, and with i 100 X suns mass to be
stable |
| 8 Nuclear fusion keeps star cool |
| 9 Gas clouds 1,000-10,000 molecules per cubic centimeter 755 hydrogen and 25%
Helium, form from being squeezed from outside, then gravity brings them together |
10 Galactic sound wave from center caused by exploding stars squeezed matter together
as it passes like stirring
up cream in a drink, that is why it is a spiral galaxy. |
| 11 PARSEC- Arc second, 3.25 light years, 206,000 X earths distance to sun |
12 In this part of space, 1 star per 5 cubic parsecs of space, on Orion nebula,
stars are 1/10 parsec apart,
10,000 stars per parsec (3), after stars born they spread out in orbit around
milky way |
| 13 Nuclear fusion at 15 million degrees |
14 Star 25X mass of sun lives for 3 million years, sun lives 10,000 million years,
and one 1/2suns sue lives
200,000 million years, sun 1/2 through life |
15 After hydrogen is used up helium turns to carbon for B years in sun and is
a red giant as big as earths orbit
spewing out more complex elements and collapses so electrons snuggled up against
nucleus and turns to white dwarf
up against nucleus and turns to white dwarf 2/3 mass of the sun today the size
of the earth, 1 cm cubed weighs a
ton, million times density of water. today sun has million X volume of earth |
| 16 A dead star 1.4 X the mass of earth collapses again and electrons fuse with
proton and makes a neutron, reverse |
| 17 beta decay and turns to neutron star 1.5X mass of sun is 10 kilometers across |
| 18 At formation of neutron star the by products are photons and neutrinos, CM(3)
weighs B tons |
| 19 A neutron star 3-4 x suns mass can't hold itself apart any more and
neutrons collapse into nothing and it turns to a black hole, sucking even photons in |
| 20 Stars 11 solar masses, 11 X suns size, turn to black holes |
| 21 Neutron stars 10 billion degrees |
22 Super novas caused by the collapse of star into neutron star and bouncing
back a little and pushing incoming
material out and neutrinos also. ?To form planets later |
| 23 70 B neutrinos pass through a square cm of earth a second |
| 24 Gold is only made in supernova |
| 25 10 B neutrinos passed through our bodies in 87 from the supernova
160,000 light years away |
| 26 Solar system born from stuff of many supernovas, 1 atom in a thousand is heavier
than lithium |
|
|
6 DNA
| 1 De-oxygenated ribose sugar- C(4)O |
| 2 Phosphate group- O(4)P |
| 3 Base (adenine, cytosine, Guanine, thymine) |
4 Millions of atoms in a DNA molecule
Backbone of chain made of alternating sugar and phosphate groups with a base
group sticking to each sugar
helical - the base holds the strands together Thymine and cytosine - 6 sided,
4 carbon and 2 nitrogen atoms
Adenine and Guanine- 6 sides, one less carbon and more hydrogen amine groups |
5 A and G 2X diameter of T and C
A and T match up and C and G match up with 3 hydrogen bonds |
| 6 It unravels and replicates |
7 The 4 bases are the 4 letters of the DNA and make 3 letter words to make 64
different words that arrange
differently to give complex messages |
8 The new strand is RNA (Ribose) until it moves out and has its own cell
Enzymes - most important proteins
Molecules that cause others to act a certain way helps chemicals bond together
like a puzzle piece, different
enzymes do different bring chemicals together, some snip them apart |
9 100 thousand Billion cells in body, 1000 X more than bright stars in milky
way
Cytoplasm- cell goo |
| 10 Human reproduces 23 sets of chromosomes, 46 total |
| 11 Chromosomes, DNA and proteins rolled up into histone balls |
| 12 If DNA unraveled it would be 1.8 meters, 75 K genes in each of the 23 chromosomes |
13 2 sets of chromosomes in every cell, so the same gene twice, that is how
recessive genes can come back, if both
parents tell you to have brown eyes you will, but if one says blue, and the other
brown, you will have blue |
| 14 Sex recombines genes to ensure mixed heritage |
| 15 3 Components to DNA |
|
|
7 Large and Small 
| 1 100 B galaxies visible |
| 2 30% disc shaped galaxies like the milky way |
| 3 %60 ellipticals, smaller and larger than milky way, some with thousand of billions
of stars |
| 4 10% irregular galaxies universe growing at 600 km per second, no center, 13
B years |
5 There are black holes millions of times more massive than the sun and shoot
out electromagnetic radiation
from quasars |
| 6 Farther light travels the longer the wave length |
| 7 1/10,000 of a second after big bang subatomic stuff formed |
8 After 500,000 years electromagnetic radiation and matter went their separate
ways, 1,000 B degrees, photons
were particle verses anti particles pairs, this happened as universe cooled
for every billion anti protons
there were a B and 1 neutrons, these leftovers formed known universe. The rest
canceled each other out and
are back ground photon radiation |
| 9 4 minutes after time zero hydrogen and helium nuclei formed, (alpha particles) |
10 300,000 after time zero the atoms formed, causing electromagnetic radiation
to move feeling through
matter. |
11 Ultimately total energy of Universe is zero because it all cancels each other
out, the negative energy
is gravity causes kinetic energy of motion, these together first forever |
| 12 At 10(-43) seconds old universe was 10 (94) grams cm (3) and 10 (-33) cm across |
| 13 Universe doubled in size in 5 B years |
| 14 Force of gravity between 2 objects infinity apart is 1 by infinity squared |
15 99% universe is dark matter, unaffected by all forces but gravity, photons,
wimps, spread out evenly in universe
unlike visible matter go through us at 100 k per second |
| 16 45 BB molecules in CM (3) of air at 0 degrees Celsius |
| 17 PROTON vs. H-ATOM SIZE: The diameter of a single proton has been measured and is found to be 10^-15 meters. The diameter of a single hydrogen atom in its ground state is 10^-10 meters. So the RATIO of the size of the hydrogen atom to the size of the proton is 10^5. |
| 18 DNA molecules have a consistant width of about 2.5 nanometers |
| 19 diameter of a C60 "buckyball" is about 10 Angstrom (1 nanometer). |
| 20 diameter of an atom ranges from about 0.1 to 0.5 nanometer |
| 21 A proton has a diameter of approximately one-millionth of a nanometer |
| 22 Diameter of red blood cell is 0.0076mm |
| 23 The diameter of the nucleus is in the range of 1.6 fm (1.6 × 10−15 m) (for a proton in light hydrogen) to about 15 fm (for the heaviest atoms. |
| 24 Central part of an atom or nucleus, has a diameter of about 10-15m or 1.6 fm in ... |
| 25 Galaxy with a diameter of about 100000 light-years containing about 200 billion stars. |
| 26 In the model km m cm diameter of Sun 1400000 23 (ball) distance from Sun to ... |
| 27 Earth's Diameter at the Equator: 7926.28 miles (12756.1 km) |
| 28 The Sun's diameter is 1.4 million kilometers |
| 29 A light-year is about 9461000000000 km. |
| 30 Diameter of the moon = 3 474.8 kilometers |
|
|
8 Big stars diameter in kilometers
| 1 Sirius 2335000 |
| 2 Vega 4315000 |
| 3 Pollux 11120000 |
| 4 Arcturus 22101000 |
| 5 Aldebaran 59770000 |
| 6 Rigel 97300000 |
| 7 Deneb 201550000 |
| 8 Pistol star 450520000 |
| 9 Betelgeuse 903500000 |
| 10 Antares 1330000000 |
| 11 W chepei 2644800000 |
| 12 Milky way galaxy 946,100,000,000,000,000 |
|
|
9 Molecules of Life
1 Polymer - Long chain molecule
Carbohydrates - Rings of carbon with hydrogen on one side and oxygen-hydrogen
on the other
sugar - with 5 carbons and 1 oxygen
DNA - Deoxyribonucleic acid
Acid- In chemical reaction, gives up hydrogen
Base- in reaction gives up OH
|
| 2 When they react together they produce water |
| 3 Were more than 3/4 water |
4 Proteins - Most important molecules in our bodies, different kinds that bond
with each other twist together like
rope |
| 5 Earths crust is %47 oxygen %28 silicon
and 8% aluminum |
6 Our bodies dry matter is %25 oxygen and 10% nitrogen proteins 16% nitrogen
Nitrogen-bonds with 3 things atoms attached to the 4 bonds of carbon |
7 Many amino acids could exist, but we have 23 kinds |
| 8 Polypeptide chains have connections on the side called radicals that give the
proteins their individuality |
9 With 23 amino acids, there is huge amount of proteins that could be made, and
big proteins bigger the English
words, one protein hemoglobin has a molecular weight of 67,000 |
10 2 kinds of proteins, long thin kind like hair, and bunched up kind
Keratin- Fibrous protein with repeating patterns, unstretched alpha keratin
and stretched beta-keratin the
bunched up unstretched kind is bone what shoes up in X-rays
Alpha helix- Key structure the peptide bond is held riding in hair they |
| 11 In softer proteins like silk, they zig zag around each other |
|
|
10 Table of Brightest Stars
| 1 Sirius -1.46 8.6 light years |
| 2 Canopus Carina -.72 100 |
| 3 Rigil Kentauras centaury, -.27 4.5 |
| 4 Arcturus Boots -.04 36 |
| 5 Vega Lyrae +.3 26 |
| 6 Capella Aurigae .08 45 |
| 7 Rigel Orionis .12 900 |
| 8 Procyon Canis minoris .38 11.4 |
| 9 Archernar Eridani .46 90 |
| 10 Betelgeus-sg Orionis .5 300 |
| 11 adar Centauri .61 520 |
| 12 Altair Aquilae .77 17 |
| 13 Aldebaron Tauri .85 68 |
| 14 Acrux Crucis .87 370 |
| 15 Antares-sg Scorpii .96 500 |
| 16 Spica Virginis .98 220 |
| 17 Pollux Geminorum 1.14 35 |
| 18 Fomalhaut Pisces Austrini 1.16 83 |
| 19 Deneb Cygni 1.25 1600 |
| 20 Mimosa Crucis 1.25 470 |
| 21 Regulus-B Leonis 1.35 85 |
| 22 Ahara Canis major 1.42 650 |
| 23 Bellitrix Orionis 1.611 450 |
|
|
11 Interesting Astronomical Numbers
1 10 Billion stars in
milky way, olympic swimming pool with drops of water
|
| 2 160K how high satellites are |
| 3 Moon 81 X smaller than earth, 15.5 CM AWAY |
4 Sun big beach ball 30 inches70 cm across and earth is 75 meters away the
size of a pea, mercury is 30M away the
size of a pinhead jupiter is 400 Meters away size of a tennis ball uranus 10
Aussie cent coin 1.5 Km away pluto
a speck 18 ks away.
Mercury - 58 M kilos 5000 K diameter solar system 4.6 B years old
Mars - Half Earths size
Saturn - 10X earths diameter
Neptune - 30X as far from sun as earth
|
| 5 Meteors burn up 100K up at 100,000Kph |
| 5 Super giants 100 - 200 X the suns diameter |
6 If the galaxy was as big as Australia stars would be almost invisible specs
200m apart and the solar system
is 20 MM across |
7 Nebula, hundreds of light years in size
Globular's- 10s of thousand to over a million stars, can be thousands per cubic
light year |
| 8 Galactic center 30K light years away |
| 9 Psychedelic guided imagery to conceptualize things |
| 10 Einstein 'The eternal mystery of
the world is its comprehensibility'. |
| 11 Avagadro's number- # of hydrogen atoms in one gram 6.022045 X 10(23) |
12 At 0 degrees Celsius one cubic centimeter of air has 4.5 X 10(19) molecules
of air and travels at 461 miles
per second or 17 K k/h, 3.5 B collisions/second
Newton's three laws- 1) object stays in motion 2) Force makes it accelerate 3)
Equal and opposite reaction
10(23)- stars in universe |
| 13 Cesium is biggest atom at .0000005 mm across, 10m to stretch across postage
stamps serrated edge |
| 14 Kelvin- atom is .1 nanometers across atom 10(-8) cm across, but nucleus 10(-13) |
15 Nucleus is 10(-15) of atom, one M of B
Isotope- Positive or negative charge atom, carbon
photon- light beam |
16 92 - Protons in Uranium, 234 weight
10(12)- photons of light hit pinhead in a second |
17 Photons keep atom from collapsing
Planck's constant- Mass of photon 6.5 X 10(-27) |
| 18 Electron mass- 9 X 10(-28)G |
| 19 We are halfway between quanta and known universe |
| 20 Something 10(-27) cm across inside sugar cube is like sugar cubes spanning
1/10 of known universe one B light years |
| 21 0 degrees Celsius oxygen molecule
moves 461 m/s, 17K KM/H |
| 22 Atom looses energy as electron moves closer to nucleus and gains it as it moves
away from nucleus |
| 23 Mass of electron is 9 X 10(-28) |
| 24 # stars in galaxy 10(11) |
| 25 So we are halfway between atom and universe |
| 26 Collapse of the wave function'? p 51 |
| 27 The more an electron is squeezed, the higher its velocity |
| 28 'Wave packet' keeps electron from hitting nucleus |
| 29 2 electrons in first level and 8 on each others |
|
|
12 Measurements
| 1 Kilometer 1000 meters |
| 2 Meter |
| 3 Centimeter .01 meter 100 in meter |
| 4 Millimeter .001 meter one thousandth of a meter. 1,000 in meter |
| 5 Micrometer (micron) one millionth of meter .000001 1,000,000 in meter |
| 6 Millimicron (nanometer) one billionth of meter .000,000,001 1,000,000,000 in meter |
| 7 Angstrom. One ten billionth of a meter. |
| 8 Picometer. One trillionth of a meter. 1,000,000,000,000 in a meter. |
| 9 Femtometer. One quadrillionth of a meter. |
| 10 Attometer. One quintillionth of a meter 10-18 |
| 11 Zeptometer. One sextillionth of a meter. 10-21 |
| 12 Yoktometer. One septillionth of a meter. 10-24 |
| 13 Sytometer = Octillionth of a meter |
| 14 Tredometer = Nonillionth |
| 15 Revometer is a decillionth of a meter |
| 16 Planck length. One Undecillionth of a meter. 10-35 |
|
|
13 Our changing planet 
1 Earth diameter 12,800 km
circumfrence 40 k/km
|
| 2 Deepest mine 4 km, deepest drill 40 km |
| 3 Inner core solid 3200 km diameter 5000 degrees Celsius |
| 4 Liquid outer core 1800 k |
| 5 Continents formed by asteroids and then spread and kept earth from losing too
much heat |
| 6 Isotopes- Uranium and such dissolving into simpler elements gives off energy
which keeps earth warm |
| 7 Mantle- 3 K km thick Lower- 2300 and upper 630, %82 earths volume and 2/3 the
mass |
| 8 Crust- 40 km thick over continents 1- km under oceans |
| 9 At 20 km, that is less than 1/3 of 1% of distance from center to surface |
| 10 75-220 down, asthenoshpere 1100 degrees Celsius, slushy rocks |
| 11 Plate tectonics not accepted till 60's |
| 12 Plates in oceans go below the surface and melt again |
| 13 Atlantic widening at 2 CM a year |
| 14 Magnetic field in north to south lines created when the molten crust cools
in mid atlantic, it picks up the
magnetism from the field |
| 15 Every few thousand years the magnetic field reverses |
| 16 Constructive - plates crash and make mountain |
| 17 Destructive - go down |
| 18 Conservative- Slide against each other |
| 19 Sometimes plates get stuck and effects all plates and causes earthquakes to
re-equalize |
20 North atlantic plates meet and rub by each other at San Andreas fault MOVES
NORTH AT 6 CMS A YEAR, IF IT STICKS
A HUNDRED YEARS, IT MOVES 6 METERS TO CATCH UP. |
| 21 Spreading sites change |
| 22 We test tectonic history with magnetic lines 600 M years ago Gondwanaland |
| 23 500 M years ago development of first fishes |
| 24 400 M years ago plants spread over continents and first reptiles evolved |
| 25 Gondwanaland split and came back together in Pangea like 400 M years ago |
| 26 250 M years Pangea broke up and mammals began |
27 65 million years ago America broke from Europe and Australia broke from Antarctica
and dinosaurs died in comet
10 km across in Ukatan |
28 Ocean 2/3 of earth, half of ocean renewed since 65 M years, 1/3rd-Volcanic
islands caused by ocean plates going
down and being spit up again in nearby areas of thin ocean crust 5 km keep,
the islands shows direction of plates
of earth |
29 Maybe life started in underwater plates of boiling water and hydrogen sulphide,
but we don't know because all
early life got recycled and didn't make fossils |
30 600 M years first shells-440 M years ago Gondwanaland went over south pole
and froze, second biggest extinction
time. |
| 31 Life on land formed by shallow oceans receding and advancing and eating plants
on the land |
32 Millipedes and cockroaches were the first land animals 300 million years ago
360-280 M years trees died and formed layer of coal |
| 33 270 M years ago, first warm blooded mammals and comet crossed and killed 90%
of life and reptiles prospered |
| 34 248-213-Reptiles dominate |
| 35 213-65 M Dinosaurs dominate and 65 the comet hits Yucatan |
36 Science-Heat- IN convection, heat transfer, heart travels inverse squarely,
it travels twice as far in 4
seconds as 2 seconds. |
|
|
14 Numbers
1 1,000 X 1 thousand = 1 million (106) |
2 1,000 X 1 million = 1 billion (109) |
3 1,000 X 1 billion = 1 trillion (1012) |
4 1,000 X 1 trillion = 1 quadrillion (1015) |
5 1,000 X 1 quadrillion = 1 quintillion (1018) |
6 1,000 X 1 quintillion = 1 sextillion (1021) |
7 1,000 X 1 sextillion = 1 septillion (1024) |
8 1,000 X 1 septillion = 1 octillion (1027) |
9 1,000 X 1 octillion = 1 nonillion (1030) |
10 1,000 X 1 nonillion = 1 decillion (1033) |
11 1,000 X 1 decillion = 1 undecillion (1036)
|
12 1,000 X 1 undecillion = 1 duodecillion (1039) |
13 Other very large numbers are:
| 1 One googol = 10100 |
| 2 One googolplex = 10googol |
| 3 One googolplexian = 10googolplex |
| 4 10-3 thousandth |
| 5 10-9 billionth |
|
|
|
15 Molecules of Life
1 Polymer - Long chain molecule
Carbohydrates - Rings of carbon with hydrogen on one side and oxygen-hydrogen
on the other
sugar - with 5 carbons and 1 oxygen
|
2 DNA - Deoxyribonucleic acid
Acid- In chemical reaction, gives up hydrogen
Base- in reaction gives up OH |
| 3 When they react together they produce water |
4 Were more than 3/4 water
Proteins - Most important molecules in our bodies, different kinds that bond
with each other twist together like
rope |
| 5 Earths crust is %47 oxygen %28 silicon
and 8% aluminum |
6 Our bodies dry matter is %25 oxygen and 10% nitrogen proteins 16% nitrogen
Nitrogen-bonds with 3 things atoms attached to the 4 bonds of carbon |
| 7 Many amino acids could exist, but we have 23 kinds |
| 8 Polypeptide chains have connections on the side called radicals that give the
proteins their individuality |
9 With 23 amino acids, there is huge amount of proteins that could be made, and
big proteins bigger the English
words, one protein hemoglobin has a molecular weight of 67,000 |
| 10 2 kinds of proteins, long thin kind like hair, and bunched up kind |
11 Keratin- Fibrous protein with repeating patterns, unstretched alpha keratin
and stretched beta-keratin the
bunched up unstretched kind is bone what shoes up in X-rays |
| 12 Alpha helix- Key structure the peptide bond is held riding in hair they |
| 13 In softer proteins like silk, they zig zag around each other |
|
|
16 Quantum Theory
| 1 Is about the compatibility of two
apparently irreconcilable opposites |
| 2 Being forced to listen without being allowed to reply is a stimulant for radical
thought |
| 3 It needs imagination |
4 Philosophy and science were disastrous for each other to explain things like
atoms of one element leaving to
become atoms of another element |
5 The model for the atom came when Rutherford shot positive charged alpha particles
into atoms and were deflected
by the nucleus, of positive charge. at -10 degrees instead of negative 1 degree.
and the micro and macro worlds
mirrored each other. |
|
|
17 Solar system plants diameter
| 1 It is 12 light hours across. Since the speed of light is 300,000 km/second or 186,000 miles/second, 12 light hours is 12,960,000,000 kilometers, or 1.296 X 10 ^ 10, or 12 billion and 960 millionkilometers, OR 8,052,970,651.4 miles. |
| 2 Earth = 12 756.2 kilometers |
| 3 Diameter of Mercury = 4879 km at its equator |
| 4 The diameter of Mars is 6792 km at the equator and 6752 km at the poles. Mean Diameter = 6772 km. |
| 5 Venus Diameter: 12103.6 km (7700 miles) ... |
| 6 Diameter in jupiter 142800 km. |
| 7 Saturn's diameter is around 75000 miles 120000 kilometers . |
| 8 Diameter of Uranus is 51118 km |
| 9 Pluto's diameter as 2274 kilometers (1413 miles) |
| 10 12.1 nm, which is enough for the membrane thickness plus a M13 virus diameter Bacteria measure from 0.2 – 0.3 microns in diameter |
| 11 Many of the spherical bacteria are about 1 micrometer in diameter |
| 12 Diameter of red blood cell 0.0076mm |
| 13 The average cell in our body is about 50 micrometers (0.05 mm) in diameter |
| 14 The diameter of human hair ranges from 17 to 181 µm. micrometer |
15 The dermis also varies in thickness depending on the location of the skin. It is .3 mm on the eyelid and 3.0 mm on the back.
Whereas the thinnest walls, about 50 nm, are found in inner cell layers. |
| 16 10 Billion stars in
milky way, olympic swimming pool with drops of water |
| 17 160K how high satellites are |
| 18 Moon 81 X smaller than earth, 15.5 CM AWAY |
| 19 Meteors burn up 100K up at 100,000Kph |
| 20 Super giants 100 - 200 X the suns diameter |
21 If the galaxy was as big as Australia stars would be almost invisible specs
200m apart and the solar system
is 20 MM across |
| 22 Nebula, hundreds of light years in size |
| 23 Globular's- 10s of thousand to over a million stars, can be thousands per cubic
light year |
| 24 Galactic center 30K light years away |
| 25 Psychedelic guided imagery to conceptualize things |
|
|
18 Table of Brightest Stars 
| 1 Sirius -1.46 8.6 light years |
| 2 Canopus Carina -.72 100 |
| 3 Rigil Kentauras centaury, -.27 4.5 |
| 4 Arcturus Boots -.04 36 |
| 5 Vega Lyrae +.3 26 |
| 6 Capella Aurigae .08 45 |
| 7 Rigel Orionis .12 900 |
| 8 Procyon Canis minoris .38 11.4 |
| 9 Archernar Eridani .46 90 |
| 10 Betelgeus-sg Orionis .5 300 |
| 11 adar Centauri .61 520 |
| 12 Altair Aquilae .77 17 |
| 13 Aldebaron Tauri .85 68 |
| 14 Acrux Crucis .87 370 |
| 15 Antares-sg Scorpii .96 500 |
| 16 Spica Virginis .98 220 |
| 17 Pollux Geminorum 1.14 35 |
| 18 Fomalhaut Pisces Austrini 1.16 83 |
| 19 Deneb Cygni 1.25 1600 |
| 20 Mimosa Crucis 1.25 470 |
| 21 Regulus-B Leonis 1.35 85 |
| 22 Ahara Canis major 1.42 650 |
| 23 Bellitrix Orionis 1.611 450 |
|
|
19 Star Systems in Constelations
| 1 Aquarius formalhout, enif |
| 2 Pisces algenib, mirach, alpheratz, scheat markab |
| 3 Aries harmal, sheratan, triangulum, almach |
| 4 Taurus Pliedes, Aldebran, Hyades, capella, orion |
| 5 Gemini Castor, pollux, athena, betelgeus, procyon |
| 6 Cancer acubens, dnoces, alphard |
| 7 Leo regulus, denebola |
| 8 Virgo prrima, vindemiatrix, arcturus, bootes, spica |
| 9 Libra pschubba, zubenelqenubi, zubeneschamali |
| 10 scorpius Antates, pschubba, sabik, shaula, lupus |
| 11 Sagittarius corona autr, teapot, nink |
| 12 Capricorn Dabih, algedi, deneb algedi |
|
|
20 Particles and Feilds
1 Electron spin opposite to each other
|
| 2 Chemical properties relate to electrons orbits, how many there are in outermost
shell |
| 3 Electron like to close their shells, that is how molecules are made, covalent
bonding |
| 4 Moving electric charge creates magnetic
field |
| 5 Light a form of electromagnetic wave, so is radio |
| 6 Electromagnetic rays travel from electron to electron |
| 7 Photons have no mass |
8 3 kinds of quarks, 2 in P and N, up and down
P = 2 ups and 1 down 2/3+2/3 = 1
N = 2 downs and 1 up, 2/3-1/3 = 0 |
9 Exist only in triplets and pairs
paris called mesons - have mass |
10 Nucleons - components of nucleus
Quantum uncertainty- life span of quarks |
11 10,000,000,000,000,000,000,000
/sec,
22 OÕ's after one |
12 High energy turns them into particles as they appear and disappear, the more
energy the shorter existence
Gluons- Keep the quarks together
Weak force- Beta decay, neutrino, intermediate vector boson |
| 13 4 FORCES- 1) Gravity 2) Nuclear 3) strong 4) weak |
| 14 4 PARTICLES- 1) Up quark 2) Down quark 3) Electron 4) Neutrino |
| 15 New big electron formed in experiments |
| 16 Field quanta with no mass 1) Gravitons 2) Photons |
| 17 Gravity decreases inverse squarely |
| 18 Photons carry electromagnetism, much stronger than gravity, but cancels itself
out with + and - poles |
19 6 X 10(24) kg is mass of Earth
strong force 1, electromagnetism is 10(-2) (1% as strong), weak force 10(-13) (100
B as strong), |
20 loops of 'string' holding quarks together 10(-33) cm in diameter,
as much smaller than atom as atom is smaller
than solar system |
| 21 String vibration corresponds to photon and graviton vibration |
|
|
|
2 Art 
|
4 Golden mean Spiral 

The golden ratio in a regular pentagon can be computed using Ptolemy's theorem .
Illustration from Luca Pacioli's De Divina Proportione applies geometric proportions to the human face.
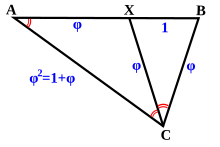
Golden triangle

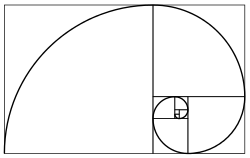


|
Golden ratio 1.618 
The golden section is a line segment divided according to the golden ratio: The total length a + b is to the longer segment a as a is to the shorter segment b.
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to (=) the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.6180339887. Other names frequently used for the golden ratio are the golden section (Latin: sectio aurea) and golden mean. Other terms encountered include extreme and mean ratio, medial section, divine proportion, divine section (Latin: sectio divina), golden proportion, golden cut, golden number, and mean of Phidias. The golden ratio is often denoted by the Greek letter phi, usually lower case (φ).
At least since the Renaissance, many artists and architects have proportioned their works to approximate the golden ratio—especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio—believing this proportion to be aesthetically pleasing. Mathematicians have studied the golden ratio because of its unique and interesting properties.
Construction of a golden rectangle
1. Construct a unit square (red).
2. Draw a line from the midpoint of one side to an opposite corner.
3. Use that line as the radius to draw an arc that defines the long dimension of the rectangle.
History 
Mathematician Mark Barr proposed using the first letter in the name of Greek sculptor Phidias, phi, to symbolize the golden ratio. Usually, the lowercase form (φ) is used. Sometimes, the uppercase form (Φ) is used for the reciprocal of the golden ratio, 1/φ. [10]
Michael Maestlin, first to publish a decimal approximation of the golden ratio, in 1597.
The golden ratio has fascinated Western intellectuals of diverse interests for at least 2,400 years:
Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over this simple ratio and its properties. But the fascination with the Golden Ratio is not confined just to mathematicians. Biologists, artists, musicians, historians, architects, psychologists, and even mystics have pondered and debated the basis of its ubiquity and appeal. In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics.
— Mario Livio , The Golden Ratio: The Story of Phi, The World's Most Astonishing Number
Ancient Greek mathematicians first studied what we now call the golden ratio because of its frequent appearance in geometry. The division of a line into "extreme and mean ratio" (the golden section) is important in the geometry of regular pentagrams and pentagons. The Greeks usually attributed discovery of this concept to Pythagoras or his followers. The regular pentagram, which has a regular pentagon inscribed within it, was the Pythagoreans' symbol.
Euclid's Elements (Greek: Στοιχεῖα) provides the first known written definition of what is now called the golden ratio: "A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less."[5] Euclid explains a construction for cutting (sectioning) a line "in extreme and mean ratio", i.e. the golden ratio.[11] Throughout the Elements, several propositions (theorems in modern terminology) and their proofs employ the golden ratio.[12] Some of these propositions show that the golden ratio is an irrational number.
The name "extreme and mean ratio" was the principal term used from the 3rd century BC[5] until about the 18th century.
The modern history of the golden ratio starts with Luca Pacioli's Divina Proportione of 1509, which captured the imagination of artists, architects, scientists, and mystics with the properties, mathematical and otherwise, of the golden ratio.
The first known approximation of the (inverse) golden ratio by a decimal fraction, stated as "about 0.6180340," was written in 1597 by Prof. Michael Maestlin of the University of Tübingen in a letter to his former student Johannes Kepler.[13]
Since the twentieth century, the golden ratio has been represented by the Greek letter Φ or φ (phi, after Phidias, a sculptor who is said to have employed it) or less commonly by τ (tau, the first letter of the ancient Greek root τομή—meaning cut).
Timeline 
Timeline according to Priya Hemenway
- Phidias (490–430 BC) made the Parthenon statues that seem to embody the golden ratio.
- Plato (427–347 BC), in his Timaeus, describes five possible regular solids (the Platonic solids: the tetrahedron, cube, octahedron, dodecahedron and icosahedron), some of which are related to the golden ratio
- Euclid (c. 325–c. 265 BC), in his Elements, gave the first recorded definition of the golden ratio, which he called, as translated into English, "extreme and mean ratio" (Greek: ἄκρος καὶ μέσος λόγος).
- Fibonacci (1170–1250) mentioned the numerical series now named after him in his Liber Abaci; the ratio of sequential elements of the Fibonacci sequence approaches the golden ratio asymptotically.
- Luca Pacioli (1445–1517) defines the golden ratio as the "divine proportion" in his Divina Proportione.
- Johannes Kepler (1571–1630) proves that the golden ratio is the limit of the ratio of consecutive Fibonacci numbers,[16] and describes the golden ratio as a "precious jewel": "Geometry has two great treasures: one is the Theorem of Pythagoras, and the other the division of a line into extreme and mean ratio; the first we may compare to a measure of gold, the second we may name a precious jewel." These two treasures are combined in the Kepler triangle.
- Charles Bonnet (1720–1793) points out that in the spiral phyllotaxis of plants going clockwise and counter-clockwise were frequently two successive Fibonacci series.
- Martin Ohm (1792–1872) is believed to be the first to use the term goldener Schnitt (golden section) to describe this ratio, in 1835.
- Edouard Lucas (1842–1891) gives the numerical sequence now known as the Fibonacci sequence its present name.
- Mark Barr (20th century) suggests the Greek letter phi (φ), the initial letter of Greek sculptor Phidias's name, as a symbol for the golden ratio.[18]
- Roger Penrose (b.1931) discovered a symmetrical pattern that uses the golden ratio in the field of aperiodic tilings, which led to new discoveries about quasicrystals.
Aesthetics 
Beginning in the Renaissance, a body of literature on the aesthetics of the golden ratio was developed. As a result, architects, artists, book designers, and others have been encouraged to use the golden ratio in the dimensional relationships of their works.
The first and most influential of these was De Divina Proportione by Luca Pacioli, a three-volume work published in 1509. Pacioli, a Franciscan friar, was known mostly as a mathematician, but he was also trained and keenly interested in art. De Divina Proportione explored the mathematics of the golden ratio. Though it is often said that Pacioli advocated the golden ratio's application to yield pleasing, harmonious proportions, Livio points out that that interpretation has been traced to an error in 1799, and that Pacioli actually advocated the Vitruvian system of rational proportions. Pacioli also saw Catholic religious significance in the ratio, which led to his work's title. Containing illustrations of regular solids by Leonardo Da Vinci, Pacioli's longtime friend and collaborator, De Divina Proportione was a major influence on generations of artists and architects alike.
Architecture 
Some studies of the Acropolis, including the Parthenon, conclude that many of its proportions approximate the golden ratio. The Parthenon's facade as well as elements of its facade and elsewhere are said to be circumscribed by golden rectangles.[19] To the extent that classical buildings or their elements are proportioned according to the golden ratio, this might indicate that their architects were aware of the golden ratio and consciously employed it in their designs. Alternatively, it is possible that the architects used their own sense of good proportion, and that this led to some proportions that closely approximate the golden ratio. On the other hand, such retrospective analyses can always be questioned on the ground that the investigator chooses the points from which measurements are made or where to superimpose golden rectangles, and that these choices affect the proportions observed.
Some scholars deny that the Greeks had any aesthetic association with golden ratio. For example, Midhat J. Gazalé says, "It was not until Euclid, however, that the golden ratio's mathematical properties were studied. In the Elements (308 BC) the Greek mathematician merely regarded that number as an interesting irrational number, in connection with the middle and extreme ratios. Its occurrence in regular pentagons and decagons was duly observed, as well as in the dodecahedron (a regular polyhedron whose twelve faces are regular pentagons). It is indeed exemplary that the great Euclid, contrary to generations of mystics who followed, would soberly treat that number for what it is, without attaching to it other than its factual properties."[20] And Keith Devlin says, "Certainly, the oft repeated assertion that the Parthenon in Athens is based on the golden ratio is not supported by actual measurements. In fact, the entire story about the Greeks and golden ratio seems to be without foundation. The one thing we know for sure is that Euclid, in his famous textbook Elements, written around 300 BC, showed how to calculate its value."[21] Near-contemporary sources like Vitruvius exclusively discuss proportions that can be expressed in whole numbers, i.e. commensurate as opposed to irrational proportions.
A geometrical analysis of the Great Mosque of Kairouan reveals a consistent application of the golden ratio throughout the design, according to Boussora and Mazouz. It is found in the overall proportion of the plan and in the dimensioning of the prayer space, the court, and the minaret. Boussora and Mazouz also examined earlier archaeological theories about the mosque, and demonstrate the geometric constructions based on the golden ratio by applying these constructions to the plan of the mosque to test their hypothesis.
The Swiss architect Le Corbusier, famous for his contributions to the modern international style, centered his design philosophy on systems of harmony and proportion. Le Corbusier's faith in the mathematical order of the universe was closely bound to the golden ratio and the Fibonacci series, which he described as "rhythms apparent to the eye and clear in their relations with one another. And these rhythms are at the very root of human activities. They resound in man by an organic inevitability, the same fine inevitability which causes the tracing out of the Golden Section by children, old men, savages and the learned."
Le Corbusier explicitly used the golden ratio in his Modulor system for the scale of architectural proportion. He saw this system as a continuation of the long tradition of Vitruvius, Leonardo da Vinci's "Vitruvian Man", the work of Leon Battista Alberti, and others who used the proportions of the human body to improve the appearance and function of architecture. In addition to the golden ratio, Le Corbusier based the system on human measurements, Fibonacci numbers, and the double unit. He took Leonardo's suggestion of the golden ratio in human proportions to an extreme: he sectioned his model human body's height at the navel with the two sections in golden ratio, then subdivided those sections in golden ratio at the knees and throat; he used these golden ratio proportions in the Modulor system. Le Corbusier's 1927 Villa Stein in Garches exemplified the Modulor system's application. The villa's rectangular ground plan, elevation, and inner structure closely approximate golden rectangles.
Another Swiss architect, Mario Botta, bases many of his designs on geometric figures. Several private houses he designed in Switzerland are composed of squares and circles, cubes and cylinders. In a house he designed in Origlio, the golden ratio is the proportion between the central section and the side sections of the house.
In a recent book, author Jason Elliot speculated that the golden ratio was used by the designers of the Naqsh-e Jahan Square and the adjacent Lotfollah mosque.
Painting 
Leonardo da Vinci's illustrations of polyhedra in De Divina Proportione (On the Divine Proportion) and his views that some bodily proportions exhibit the golden ratio have led some scholars to speculate that he incorporated the golden ratio in his paintings. But the suggestion that his Mona Lisa, for example, employs golden ratio proportions, is not supported by anything in Leonardo's own writings.
Salvador Dalí explicitly used the golden ratio in his masterpiece, The Sacrament of the Last Supper. The dimensions of the canvas are a golden rectangle. A huge dodecahedron, with edges in golden ratio to one another, is suspended above and behind Jesus and dominates the composition.
Mondrian used the golden section extensively in his geometrical paintings.
A statistical study on 565 works of art of different great painters, performed in 1999, found that these artists had not used the golden ratio in the size of their canvases. The study concluded that the average ratio of the two sides of the paintings studied is 1.34, with averages for individual artists ranging from 1.04 (Goya) to 1.46 (Bellini). On the other hand, Pablo Tosto listed over 350 works by well-known artists, including more than 100 which have canvasses with golden rectangle and root-5 proportions, and others with proportions like root-2, 3, 4, and 6.
According to Jan Tschichold, "There was a time when deviations from the truly beautiful page proportions 2:3, 1:√3, and the Golden Section were rare. Many books produced between 1550 and 1770 show these proportions exactly, to within half a millimetre."
Music 
James Tenney reconceived his piece For Ann (rising), which consists of up to twelve computer-generated upwardly glissandoing tones (see Shepard tone), as having each tone start so it is the golden ratio (in between an equal tempered minor and major sixth) below the previous tone, so that the combination tones produced by all consecutive tones are a lower or higher pitch already, or soon to be, produced.
Ernő Lendvai analyzes Béla Bartók's works as being based on two opposing systems, that of the golden ratio and the acoustic scale,[36] though other music scholars reject that analysis. In Bartok's Music for Strings, Percussion and Celesta the xylophone progression occurs at the intervals 1:2:3:5:8:5:3:2:1. French composer Erik Satie used the golden ratio in several of his pieces, including Sonneries de la Rose+Croix.
The golden ratio is also apparent in the organization of the sections in the music of Debussy's Reflets dans l'eau (Reflections in Water), from Images (1st series, 1905), in which "the sequence of keys is marked out by the intervals 34, 21, 13 and 8, and the main climax sits at the phi position."
The musicologist Roy Howat has observed that the formal boundaries of La Mer correspond exactly to the golden section. Trezise finds the intrinsic evidence "remarkable," but cautions that no written or reported evidence suggests that Debussy consciously sought such proportions. Also, many works of Chopin, mainly Etudes (studies) and Nocturnes, are formally based on the golden ratio. This results in the biggest climax of both musical expression and technical difficulty after about 2/3 of the piece.[citation needed]
Pearl Drums positions the air vents on its Masters Premium models based on the golden ratio. The company claims that this arrangement improves bass response and has applied for a patent on this innovation.
In the opinion of author Leon Harkleroad, "Some of the most misguided attempts to link music and mathematics have involved Fibonacci numbers and the related golden ratio."
Nature 
Adolf Zeising, whose main interests were mathematics and philosophy, found the golden ratio expressed in the arrangement of branches along the stems of plants and of veins in leaves. He extended his research to the skeletons of animals and the branchings of their veins and nerves, to the proportions of chemical compounds and the geometry of crystals, even to the use of proportion in artistic endeavors. In these phenomena he saw the golden ratio operating as a universal law. In connection with his scheme for golden-ratio-based human body proportions, Zeising wrote in 1854 of a universal law "in which is contained the ground-principle of all formative striving for beauty and completeness in the realms of both nature and art, and which permeates, as a paramount spiritual ideal, all structures, forms and proportions, whether cosmic or individual, organic or inorganic, acoustic or optical; which finds its fullest realization, however, in the human form." Need quotation on talk to verify
Geometry
The number φ turns up frequently in geometry, particularly in figures with pentagonal symmetry. The length of a regular pentagon's diagonal is φ times its side. The vertices of a regular icosahedron are those of three mutually orthogonal golden rectangles.
There is no known general algorithm to arrange a given number of nodes evenly on a sphere, for any of several definitions of even distribution (see, for example, Thomson problem). However, a useful approximation results from dividing the sphere into parallel bands of equal area and placing one node in each band at longitudes spaced by a golden section of the circle, i.e. 360°/φ ≅ 222.5°. This method was used to arrange the 1500 mirrors of the student-participatory satellite Starshine-3.[46]
Golden triangle, pentagon and pentagram
Golden triangle 
The golden triangle can be characterised as an isosceles triangle ABC with the property that bisecting the angle C produces a new triangle CXB which is a similar triangle to the original.
If angle BCX = α, then XCA = α because of the bisection, and CAB = α because of the similar triangles; ABC = 2α from the original isosceles symmetry, and BXC = 2α by similarity. The angles in a triangle add up to 180°, so 5α = 180, giving α = 36°. So the angles of the golden triangle are thus 36°-72°-72°. The angles of the remaining obtuse isosceles triangle AXC (sometimes called the golden gnomon) are 36°-36°-108°.
Suppose XB has length 1, and we call BC length φ. Because of the isosceles triangles BC=XC and XC=XA, so these are also length φ. Length AC = AB, therefore equals φ+1. But triangle ABC is similar to triangle CXB, so AC/BC = BC/BX, and so AC also equals φ2. Thus φ2 = φ+1, confirming that φ is indeed the golden ratio.
Pentagram 
The golden ratio plays an important role in regular pentagons and pentagrams. Each intersection of edges sections other edges in the golden ratio. Also, the ratio of the length of the shorter segment to the segment bounded by the 2 intersecting edges (a side of the pentagon in the pentagram's center) is φ, as the four-color illustration shows.
The pentagram includes ten isosceles triangles: five acute and five obtuse isosceles triangles. In all of them, the ratio of the longer side to the shorter side is φ. The acute triangles are golden triangles. The obtuse isosceles triangles are golden gnomon.
Ptolemy's theorem
The golden ratio can also be confirmed by applying Ptolemy's theorem to the quadrilateral formed by removing one vertex from a regular pentagon. If the quadrilateral's long edge and diagonals are b, and short edges are a, then Ptolemy's theorem gives b2 = a2 + ab which yields
Scalenity of triangles
Consider a triangle with sides of lengths a, b, and c in decreasing order. Define the "scalenity" of the triangle to be the smaller of the two ratios a/b and b/c. The scalenity is always less than φ and can be made as close as desired to φ.[47]
Relationship to Fibonacci sequence
Approximate and true golden spirals. The green spiral is made from quarter-circles tangent to the interior of each square, while the red spiral is a Golden Spiral, a special type of logarithmic spiral. Overlapping portions appear yellow. The length of the side of a larger square to the next smaller square is in the golden ratio.
A Fibonacci spiral that approximates the golden spiral, using Fibonacci sequence square sizes up to 34.
The mathematics of the golden ratio and of the Fibonacci sequence are intimately interconnected. The Fibonacci sequence is:
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …
The closed-form expression (known as Binet's formula, even though it was already known by Abraham de Moivre) for the Fibonacci sequence involves the golden ratio:
The golden ratio is the limit of the ratios of successive terms of the Fibonacci sequence (or any Fibonacci-like sequence), as originally shown by Kepler:[16]
Therefore, if a Fibonacci number is divided by its immediate predecessor in the sequence, the quotient approximates φ; e.g., 987/610 ≈ 1.6180327868852. These approximations are alternately lower and higher than φ, and converge on φ as the Fibonacci numbers increase, and:
However, this is no special property of φ, because polynomials in any solution x to a quadratic equation can be reduced in an analogous manner, by applying:
for given coefficients a, b such that x satisfies the equation. Even more generally, any rational function (with rational coefficients) of the root of an irreducible nth-degree polynomial over the rationals can be reduced to a polynomial of degree n ‒ 1. Phrased in terms of field theory, if α is a root of an irreducible nth-degree polynomial, then  has degree n over has degree n over  , with basis , with basis  . .
Other properties
The golden ratio has the simplest expression (and slowest convergence) as a continued fraction expansion of any irrational number (see Alternate forms above). It is, for that reason, one of the worst cases of Lagrange's approximation theorem. This may be the reason angles close to the golden ratio often show up in phyllotaxis (the growth of plants).
The defining quadratic polynomial and the conjugate relationship lead to decimal values that have their fractional part in common with
The sequence of powers of φ contains these values 0.618…, 1.0, 1.618…, 2.618…; more generally, any power of φ is equal to the sum of the two immediately preceding powers:
As a result, one can easily decompose any power of φ into a multiple of φ and a constant. The multiple and the constant are always adjacent Fibonacci numbers. This leads to another property of the positive powers of φ:
When the golden ratio is used as the base of a numeral system (see Golden ratio base, sometimes dubbed phinary or φ-nary), every integer has a terminating representation, despite φ being irrational, but every fraction has a non-terminating representation.
The golden ratio is a fundamental unit of the algebraic number field  and is a Pisot–Vijayaraghavan number.[48] and is a Pisot–Vijayaraghavan number.[48]
The golden ratio also appears in hyperbolic geometry, as the maximum distance from a point on one side of an ideal triangle to the closer of the other two sides: this distance, the side length of the equilateral triangle formed by the points of tangency of a circle inscribed within the ideal triangle, is 4 ln φ.[49]
Decimal expansion
The golden ratio's decimal expansion can be calculated directly from the expression
with √5 ≈ 2.2360679774997896964. The square root of 5 can be calculated with the Babylonian method, starting with an initial estimate such as xφ = 2 and iterating
for n = 1, 2, 3, …, until the difference between xn and xn−1 becomes zero, to the desired number of digits.
The Babylonian algorithm for √5 is equivalent to Newton's method for solving the equation x2 − 5 = 0. In its more general form, Newton's method can be applied directly to any algebraic equation, including the equation x2 − x − 1 = 0 that defines the golden ratio. This gives an iteration that converges to the golden ratio itself,
for an appropriate initial estimate xφ such as xφ = 1. A slightly faster method is to rewrite the equation as x − 1 − 1/x = 0, in which case the Newton iteration becomes
These iterations all converge quadratically; that is, each step roughly doubles the number of correct digits. The golden ratio is therefore relatively easy to compute with arbitrary precision. The time needed to compute n digits of the golden ratio is proportional to the time needed to divide two n-digit numbers. This is considerably faster than known algorithms for the transcendental numbers π and e.
An easily programmed alternative using only integer arithmetic is to calculate two large consecutive Fibonacci numbers and divide them. The ratio of Fibonacci numbers F25001 and F25000, each over 5000 digits, yields over 10,000 significant digits of the golden ratio.
Millions of digits of φ are available (sequence A001622 in OEIS). See the web page of Alexis Irlande for the 17,000,000,000 first digits
Pyramids 
A regular square pyramid is determined by its medial right triangle, whose edges are the pyramid's apothem (a), semi-base (b), and height (h); the face inclination angle is also marked. Mathematical proportions b:h:a of  and  and  are of particular interest in relation to Egyptian pyramids.
Both Egyptian pyramids and those mathematical regular square pyramids that resemble them can be analyzed with respect to the golden ratio and other ratios.
Mathematical pyramids and triangles
A pyramid in which the apothem (slant height along the bisector of a face) is equal to φ times the semi-base (half the base width) is sometimes called a golden pyramid. The isosceles triangle that is the face of such a pyramid can be constructed from the two halves of a diagonally split golden rectangle (of size semi-base by apothem), joining the medium-length edges to make the apothem. The height of this pyramid is times the semi-base (that is, the slope of the face is ); the square of the height is equal to the area of a face, φ times the square of the semi-base.
The medial right triangle of this "golden" pyramid (see diagram), with sides is interesting in its own right, demonstrating via the Pythagorean theorem the relationship or . This "Kepler triangle" is the only right triangle proportion with edge lengths in geometric progression,[52] just as the 3–4–5 triangle is the only right triangle proportion with edge lengths in arithmetic progression. The angle with tangent corresponds to the angle that the side of the pyramid makes with respect to the ground, 51.827… degrees (51° 49' 38").
A nearly similar pyramid shape, but with rational proportions, is described in the Rhind Mathematical Papyrus (the source of a large part of modern knowledge of ancient Egyptian mathematics), based on the 3:4:5 triangle; the face slope corresponding to the angle with tangent 4/3 is 53.13 degrees (53 degrees and 8 minutes). The slant height or apothem is 5/3 or 1.666… times the semi-base. The Rhind papyrus has another pyramid problem as well, again with rational slope (expressed as run over rise). Egyptian mathematics did not include the notion of irrational numbers,[56] and the rational inverse slope (run/rise, multiplied by a factor of 7 to convert to their conventional units of palms per cubit) was used in the building of pyramids.
Another mathematical pyramid with proportions almost identical to the "golden" one is the one with perimeter equal to 2π times the height, or h:b = 4:π. This triangle has a face angle of 51.854° (51°51'), very close to the 51.827° of the Kepler triangle. This pyramid relationship corresponds to the coincidental relationship .
Egyptian pyramids very close in proportion to these mathematical pyramids are known.
Egyptian pyramids
In the mid nineteenth century, Röber studied various Egyptian pyramids including Khafre, Menkaure and some of the Giza, Sakkara and Abusir groups, and was interpreted as saying that half the base of the side of the pyramid is the middle mean of the side, forming what other authors identified as the Kepler triangle; many other mathematical theories of the shape of the pyramids have also been explored.
One Egyptian pyramid is remarkably close to a "golden pyramid" – the Great Pyramid of Giza (also known as the Pyramid of Cheops or Khufu). Its slope of 51° 52' is extremely close to the "golden" pyramid inclination of 51° 50' and the π-based pyramid inclination of 51° 51'; other pyramids at Giza (Chephren, 52° 20', and Mycerinus, 50° 47') are also quite close. Whether the relationship to the golden ratio in these pyramids is by design or by accident remains controversial. Several other Egyptian pyramids are very close to the rational 3:4:5 shape.
Adding fuel to controversy over the architectural authorship of the Great Pyramid, Eric Temple Bell, mathematician and historian, claimed in 1950 that Egyptian mathematics would not have supported the ability to calculate the slant height of the pyramids, or the ratio to the height, except in the case of the 3:4:5 pyramid, since the 3:4:5 triangle was the only right triangle known to the Egyptians and they did not know the Pythagorean theorem nor any way to reason about irrationals such as π or φ.
Michael Rice asserts that principal authorities on the history of Egyptian architecture have argued that the Egyptians were well acquainted with the golden ratio and that it is part of mathematics of the Pyramids, citing Giedon (1957). Historians of science have always debated whether the Egyptians had any such knowledge or not, contending rather that its appearance in an Egyptian building is the result of chance.
In 1859, the pyramidologist John Taylor claimed that, in the Great Pyramid of Giza, the golden ratio is represented by the ratio of the length of the face (the slope height), inclined at an angle θ to the ground, to half the length of the side of the square base, equivalent to the secant of the angle θ.[61] The above two lengths were about 186.4 and 115.2 meters respectively. The ratio of these lengths is the golden ratio, accurate to more digits than either of the original measurements. Similarly, Howard Vyse, according to Matila Ghyka,[62] reported the great pyramid height 148.2 m, and half-base 116.4 m, yielding 1.6189 for the ratio of slant height to half-base, again more accurate than the data variability.
Disputed sightings
Examples of disputed observations of the golden ratio include the following:
- Historian John Man states that the pages of the Gutenberg Bible were "based on the golden section shape". However, according to Man's own measurements, the ratio of height to width was 1.45.
- In 1991, Jean-Claude Perez proposed a connection between DNA base sequences and gene sequences and the golden ratio.[64][65] Another such connection, between the Fibonacci numbers and golden ratio and Chargaff's second rule concerning the proportions of nucleobases in the human genome, was proposed in 2007.
- Australian sculptor Andrew Rogers's 50-ton stone and gold sculpture entitled Ratio, installed outdoors in Jerusalem Despite the sculpture's sometimes being referred to as "Golden Ratio," it is not proportioned according to the golden ratio, and the sculptor does not call it that: the height of each stack of stones, beginning from either end and moving toward the center, is the beginning of the Fibonacci sequence: 1, 1, 2, 3, 5, 8. His sculpture Ascend in Sri Lanka, also in his Rhythms of Life series, is similarly constructed, with heights 1, 1, 2, 3, 5, 8, 13, but no descending side.
- Some specific proportions in the bodies of many animals (including humans and parts of the shells of mollusks and cephalopods are often claimed to be in the golden ratio. There is actually a large variation in the real measures of these elements in specific individuals, and the proportion in question is often significantly different from the golden ratio The ratio of successive phalangeal bones of the digits and the metacarpal bone has been said to approximate the golden ratio. The nautilus shell, the construction of which proceeds in a logarithmic spiral, is often cited, usually with the idea that any logarithmic spiral is related to the golden ratio, but sometimes with the claim that each new chamber is proportioned by the golden ratio relative to the previous one;[71] however, measurements of nautilus shells do not support this claim.
- The proportions of different plant components (numbers of leaves to branches, diameters of geometrical figures inside flowers) are often claimed to show the golden ratio proportion in several species. In practice, there are significant variations between individuals, seasonal variations, and age variations in these species. While the golden ratio may be found in some proportions in some individuals at particular times in their life cycles, there is no consistent ratio in their proportions.[citation needed]
- In investing, some practitioners of technical analysis use the golden ratio to indicate support of a price level, or resistance to price increases, of a stock or commodity; after significant price changes up or down, new support and resistance levels are supposedly found at or near prices related to the starting price via the golden ratio. The use of the golden ratio in investing is also related to more complicated patterns described by Fibonacci numbers; see, e.g. Elliott wave principle. See Fibonacci retracement. However, other market analysts have published analyses suggesting that these percentages and patterns are not supported by the data.
- In 2003 Weiss and Weiss came on a background of psychometric data and theoretical considerations to the conclusion that the golden ratio underlies the clock cycle of brain waves. In 2008 this was empirically confirmed by a group of neurobiologists
- In 2010 the journal Science reported that the golden ratio is present at the atomic scale in the magnetic resonance of spins in cobalt niobate atoms.
|
|
|
|
5 Nature 
|
6 Types of Shapes 
1 Five Platonic Solids 
|
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and angles.
There are precisely five Platonic solids (shown below).
The name of each figure is derived from its number of faces: respectively 4, 6, 8, 12, and 20.
The aesthetic beauty and symmetry of the Platonic solids have made them a favorite subject of geometers for thousands of years. They are named for the ancient Greek philosopher Plato who theorized that the classical elements were constructed from the regular solids.
History
The Platonic solids have been known since antiquity. Ornamented models of them can be found among the carved stone balls created by the late neolithic people of Scotland at least 1000 years before Plato (Atiyah and Sutcliffe 2003). Dice go back to the dawn of civilization with shapes that augured formal charting of Platonic solids.
The ancient Greeks studied the Platonic solids extensively. Some sources (such as Proclus) credit Pythagoras with their discovery. Other evidence suggests he may have only been familiar with the tetrahedron, cube, and dodecahedron, and that the discovery of the octahedron and icosahedron belong to Theaetetus, a contemporary of Plato. In any case, Theaetetus gave a mathematical description of all five and may have been responsible for the first known proof that there are no other convex regular polyhedra.
The Platonic solids feature prominently in the philosophy of Plato for whom they are named. Plato wrote about them in the dialogue Timaeus c.360 B.C. in which he associated each of the four classical elements (earth, air, water, and fire) with a regular solid. Earth was associated with the cube, air with the octahedron, water with the icosahedron, and fire with the tetrahedron. There was intuitive justification for these associations: the heat of fire feels sharp and stabbing (like little tetrahedra). Air is made of the octahedron; its minuscule components are so smooth that one can barely feel it. Water, the icosahedron, flows out of one's hand when picked up, as if it is made of tiny little balls. By contrast, a highly un-spherical solid, the hexahedron (cube) represents earth. These clumsy little solids cause dirt to crumble and break when picked up, in stark difference to the smooth flow of water. The fifth Platonic solid, the dodecahedron, Plato obscurely remarks, "...the god used for arranging the constellations on the whole heaven". Aristotle added a fifth element, aithêr (aether in Latin, "ether" in English) and postulated that the heavens were made of this element, but he had no interest in matching it with Plato's fifth solid.
Euclid gave a complete mathematical description of the Platonic solids in the Elements; the last book (Book XIII) of which is devoted to their properties. Propositions 13–17 in Book XIII describe the construction of the tetrahedron, octahedron, cube, icosahedron, and dodecahedron in that order. For each solid Euclid finds the ratio of the diameter of the circumscribed sphere to the edge length. In Proposition 18 he argues that there are no further convex regular polyhedra. Andreas Speiser has advocated the view that the construction of the 5 regular solids is the chief goal of the deductive system canonized in "Elements". Much of the information in Book XIII is probably derived from the work of Theaetetus.
In the 16th century, the German astronomer Johannes Kepler attempted to find a relation between the five extraterrestrial planets known at that time and the five Platonic solids. In Mysterium Cosmographicum, published in 1596, Kepler laid out a model of the solar system in which the five solids were set inside one another and separated by a series of inscribed and circumscribed spheres. The six spheres each corresponded to one of the planets (Mercury, Venus, Earth, Mars, Jupiter, and Saturn). The solids were ordered with the innermost being the octahedron, followed by the icosahedron, dodecahedron, tetrahedron, and finally the cube. In this way the structure of the solar system and the distance relationships between the planets was dictated by the Platonic solids. In the end, Kepler's original idea had to be abandoned, but out of his research came the recognition that the orbits of planets are ellipses rather than circles, as well as his two laws of orbital dynamics, changing the courses of physics and astronomy, plus the discovery of the Kepler solids.
Combinatorial properties
A convex polyhedron is a Platonic solid if and only if
Each Platonic solid can therefore be denoted by a symbol {p, q} where
- p = the number of edges of each face (or the number of vertices of each face) and
- q = the number of faces meeting at each vertex (or the number of edges meeting at each vertex).
The symbol {p, q}, called the Schläfli symbol, gives a combinatorial description of the polyhedron. The Schläfli symbols of the five Platonic solids are given in the table below.
All other combinatorial information about these solids, such as total number of vertices (V), edges (E), and faces (F), can be determined from p and q. Since any edge joins two vertices and has two adjacent faces we must have:
The other relationship between these values is given by Euler's formula:
This nontrivial fact can be proved in a great variety of ways (in algebraic topology it follows from the fact that the Euler characteristic of the sphere is 2). Together these three relationships completely determine V, E, and F:
Note that swapping p and q interchanges F and V while leaving E unchanged (For a geometric interpretation of this fact see the section on dual polyhedra below).
Geometric proof
The following geometric argument is very similar to the one given by Euclid in the Elements:
- Each vertex of the solid must coincide with one vertex each of at least three faces.
- At each vertex of the solid, the total, among the adjacent faces, of the angles between their respective adjacent sides must be less than 360°.
- The angles at all vertices of all faces of a Platonic solid are identical, so each vertex of each face must contribute less than 360°/3=120°.
- Regular polygons of six or more sides have only angles of 120° or more, so the common face must be the triangle, square, or pentagon. And for:
- Triangular faces: each vertex of a regular triangle is 60°, so a shape may have 3, 4, or 5 triangles meeting at a vertex; these are the tetrahedron, octahedron, and icosahedron respectively.
- Square faces: each vertex of a square is 90°, so there is only one arrangement possible with three faces at a vertex, the cube.
- Pentagonal faces: each vertex is 108°; again, only one arrangement, of three faces at a vertex is possible, the dodecahedron.
Topological proof
A purely topological proof can be made using only combinatorial information about the solids. The key is Euler's observation that V − E + F = 2, and the fact that pF = 2E = qV. Combining these equations one obtains the equation
Simple algebraic manipulation then gives
Since E is strictly positive we must have
Using the fact that p and q must both be at least 3, one can easily see that there are only five possibilities for {p, q}:
Geometric properties 
Angles
There are a number of angles associated with each Platonic solid. The dihedral angle is the interior angle between any two face planes. The dihedral angle, θ, of the solid {p,q} is given by the formula
This is sometimes more conveniently expressed in terms of the tangent by
The quantity h is 4, 6, 6, 10, and 10 for the tetrahedron, cube, octahedron, dodecahedron, and icosahedron respectively.
The angular deficiency at the vertex of a polyhedron is the difference between the sum of the face-angles at that vertex and 2π. The defect, δ, at any vertex of the Platonic solids {p,q} is
By a theorem of Descartes, this is equal to 4π divided by the number of vertices (i.e. the total defect at all vertices is 4π).
The 3-dimensional analog of a plane angle is a solid angle. The solid angle, Ω, at the vertex of a Platonic solid is given in terms of the dihedral angle by
This follows from the spherical excess formula for a spherical polygon and the fact that the vertex figure of the polyhedron {p,q} is a regular q-gon.
The solid angle of a face subtended from the center of a platonic solid is equal to the solid angle of a full sphere (4π steradians) divided by the number of faces. Note that this is equal to the angular deficiency of its dual.
The various angles associated with the Platonic solids are tabulated below. The numerical values of the solid angles are given in steradians. The constant φ = (1+√5)/2 is the golden ratio.
Radii, area, and volume
Another virtue of regularity is that the Platonic solids all possess three concentric spheres:
The radii of these spheres are called the circumradius, the midradius, and the inradius. These are the distances from the center of the polyhedron to the vertices, edge midpoints, and face centers respectively. The circumradius R and the inradius r of the solid {p, q} with edge length a are given by
where θ is the dihedral angle. The midradius ρ is given by
where h is the quantity used above in the definition of the dihedral angle (h = 4, 6, 6, 10, or 10). Note that the ratio of the circumradius to the inradius is symmetric in p and q:
The surface area, A, of a Platonic solid {p, q} is easily computed as area of a regular p-gon times the number of faces F. This is:
The volume is computed as F times the volume of the pyramid whose base is a regular p-gon and whose height is the inradius r. That is,
The following table lists the various radii of the Platonic solids together with their surface area and volume. The overall size is fixed by taking the edge length, a, to be equal to 2.
The constants φ and ξ in the above are given by
Among the Platonic solids, either the dodecahedron or the icosahedron may be seen as the best approximation to the sphere. The icosahedron has the largest number of faces, the largest dihedral angle, and it hugs its inscribed sphere the tightest. The dodecahedron, on the other hand, has the smallest angular defect, the largest vertex solid angle, and it fills out its circumscribed sphere the most.
Symmetry 
Dual polyhedra
Every polyhedron has a dual polyhedron with faces and vertices interchanged. The dual of every Platonic solid is another Platonic solid, so that we can arrange the five solids into dual pairs.
- The tetrahedron is self-dual (i.e. its dual is another tetrahedron).
- The cube and the octahedron form a dual pair.
- The dodecahedron and the icosahedron form a dual pair.
If a polyhedron has Schläfli symbol {p, q}, then its dual has the symbol {q, p}. Indeed every combinatorial property of one Platonic solid can be interpreted as another combinatorial property of the dual.
One can construct the dual polyhedron by taking the vertices of the dual to be the centers of the faces of the original figure. The edges of the dual are formed by connecting the centers of adjacent faces in the original. In this way, the number of faces and vertices is interchanged, while the number of edges stays the same.
More generally, one can dualize a Platonic solid with respect to a sphere of radius d concentric with the solid. The radii (R, ρ, r) of a solid and those of its dual (R*, ρ*, r*) are related by
It is often convenient to dualize with respect to the midsphere (d = ρ) since it has the same relationship to both polyhedra. Taking d2 = Rr gives a dual solid with the same circumradius and inradius (i.e. R* = R and r* = r).
Symmetry groups
In mathematics, the concept of symmetry is studied with the notion of a mathematical group. Every polyhedron has an associated symmetry group, which is the set of all transformations (Euclidean isometries) which leave the polyhedron invariant. The order of the symmetry group is the number of symmetries of the polyhedron. One often distinguishes between the full symmetry group, which includes reflections, and the proper symmetry group, which includes only rotations.
The symmetry groups of the Platonic solids are known as polyhedral groups (which are a special class of the point groups in three dimensions). The high degree of symmetry of the Platonic solids can be interpreted in a number of ways. Most importantly, the vertices of each solid are all equivalent under the action of the symmetry group, as are the edges and faces. One says the action of the symmetry group is transitive on the vertices, edges, and faces. In fact, this is another way of defining regularity of a polyhedron: a polyhedron is regular if and only if it is vertex-uniform, edge-uniform, and face-uniform.
There are only three symmetry groups associated with the Platonic solids rather than five, since the symmetry group of any polyhedron coincides with that of its dual. This is easily seen by examining the construction of the dual polyhedron. Any symmetry of the original must be a symmetry of the dual and vice-versa. The three polyhedral groups are:
The orders of the proper (rotation) groups are 12, 24, and 60 respectively — precisely twice the number of edges in the respective polyhedra. The orders of the full symmetry groups are twice as much again (24, 48, and 120). See (Coxeter 1973) for a derivation of these facts.
The following table lists the various symmetry properties of the Platonic solids. The symmetry groups listed are the full groups with the rotation subgroups given in parenthesis (likewise for the number of symmetries). Wythoff's kaleidoscope construction is a method for constructing polyhedra directly from their symmetry groups. We list for reference Wythoff's symbol for each of the Platonic solids.
In nature and technology
The tetrahedron, cube, and octahedron all occur naturally in crystal structures. These by no means exhaust the numbers of possible forms of crystals. However, neither the regular icosahedron nor the regular dodecahedron are amongst them. One of the forms, called the pyritohedron (named for the group of minerals of which it is typical) has twelve pentagonal faces, arranged in the same pattern as the faces of the regular dodecahedron. The faces of the pyritohedron are, however, not regular, so the pyritohedron is also not regular.
Circogonia icosahedra, a species of Radiolaria, shaped like a regular icosahedron.
In the early 20th century, Ernst Haeckel described (Haeckel, 1904) a number of species of Radiolaria, some of whose skeletons are shaped like various regular polyhedra. Examples include Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus and Circorrhegma dodecahedra. The shapes of these creatures should be obvious from their names.
Many viruses, such as the herpes virus, have the shape of a regular icosahedron. Viral structures are built of repeated identical protein subunits and the icosahedron is the easiest shape to assemble using these subunits. A regular polyhedron is used because it can be built from a single basic unit protein used over and over again; this saves space in the viral genome.
In meteorology and climatology, global numerical models of atmospheric flow are of increasing interest which employ grids that are based on an icosahedron (refined by triangulation) instead of the more commonly used longitude/latitude grid. This has the advantage of evenly distributed spatial resolution without singularities (i.e. the poles) at the expense of somewhat greater numerical difficulty.
Geometry of space frames is often based on platonic solids. In MERO system, Platonic solids are used for naming convention of various space frame configurations. For example ½O+T refers to a configuration made of one half of octahedron and a tetrahedron.
Several Platonic hydrocarbons have been synthesised, including cubane and dodecahedrane.
Platonic solids are often used to make dice, because dice of these shapes can be made fair. 6-sided dice are very common, but the other numbers are commonly used in role-playing games. Such dice are commonly referred to as dn where n is the number of faces (d8, d20, etc.); see dice notation for more details.
These shapes frequently show up in other games or puzzles. Puzzles similar to a Rubik's Cube come in all five shapes — see magic polyhedra.
Related polyhedra and polytopes
Uniform polyhedra
There exist four regular polyhedra which are not convex, called Kepler-Poinsot polyhedra. These all have icosahedral symmetry and may be obtained as stellations of the dodecahedron and the icosahedron.
The next most regular convex polyhedra after the Platonic solids are the cuboctahedron, which is a rectification of the cube and the octahedron, and the icosidodecahedron, which is a rectification of the dodecahedron and the icosahedron (the rectification of the self-dual tetrahedron is a regular octahedron). These are both quasi-regular meaning that they are vertex- and edge-uniform and have regular faces, but the faces are not all congruent (coming in two different classes). They form two of the thirteen Archimedean solids, which are the convex uniform polyhedra with polyhedral symmetry.
The uniform polyhedra form a much broader class of polyhedra. These figures are vertex-uniform and have one or more types of regular or star polygons for faces. These include all the polyhedra mentioned above together with an infinite set of prisms, an infinite set of antiprisms, and 53 other non-convex forms.
The Johnson solids are convex polyhedra which have regular faces but are not uniform.
Tessellations
The three regular tessellations of the plane are closely related to the Platonic solids. Indeed, one can view the Platonic solids as the five regular tessellations of the sphere. This is done by projecting each solid onto a concentric sphere. The faces project onto regular spherical polygons which exactly cover the sphere. One can show that every regular tessellation of the sphere is characterized by a pair of integers {p, q} with 1/p + 1/q > 1/2. Likewise, a regular tessellation of the plane is characterized by the condition 1/p + 1/q = 1/2. There are three possibilities:
In a similar manner one can consider regular tessellations of the hyperbolic plane. These are characterized by the condition 1/p + 1/q < 1/2. There is an infinite family of such tessellations.
Higher dimensions
In more than three dimensions, polyhedra generalize to polytopes, with higher-dimensional convex regular polytopes being the equivalents of the three-dimensional Platonic solids.
In the mid-19th century the Swiss mathematician Ludwig Schläfli discovered the four-dimensional analogues of the Platonic solids, called convex regular 4-polytopes. There are exactly six of these figures; five are analogous to the Platonic solids, while the sixth one, the 24-cell, has no lower-dimensional analogue.
In all dimensions higher than four, there are only three convex regular polytopes: the simplex, the hypercube, and the cross-polytope. In three dimensions, these coincide with the tetrahedron, the cube, and the octahedron.
|
|
|
|
|
|
|